Exploitation des observations Obtenues avec un sky Brightness monitor au dôme C
Diffusion
Toutefois, pour des explications plus approfondies, vous pouvez vous reporter à notre rapport de stage (ici).
1. Généralité sur la diffusion
La diffusion se produit lorsque la lumière
rencontre des particules en
traversant un milieu transparent. Dans l'atmosphère, les
molécules de l'air diffusent la lumière.
La
source (ici, le Soleil) émet un rayonnement. Ces rayons sont
absorbés par des particules
appelés diffuseurs puis réemits dans toutes les
directions.
Domaine de longueurs d'ondes de la lumière :
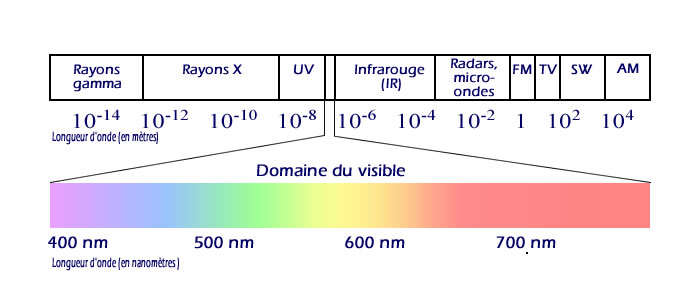
Plus la longueur d'onde est petite, plus la diffusion est importante. En fait, dans l'atmosphère terrestre, le bleu est diffusé jusqu'à huit fois plus que le rouge. C'est grâce au phénomène de diffusion de la lumière que notre ciel est lumineux durant la journée.
Le Soleil émet une émission de corps noir centré sur le jaune. Quand le soleil est haut dans le ciel, sa couleur est peu affectée par l'absorption atmosphérique et il nous apparait jaune.
En traversant l'atmosphère terrestre, la lumière est diffusée par l'air et les aérosols qu'elle contient. Le ciel est complètement éclairé de bleu, alors que les autres couleurs nous arrivent presque directement du Soleil.
Diffusion de la lumière : La composante bleue est la plus diffusée
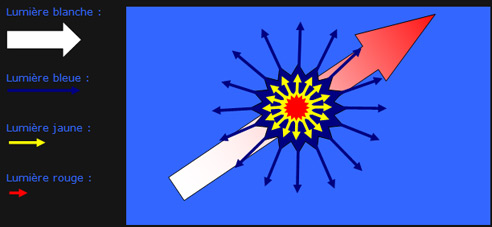
Lorsque le Soleil est bas sur l'horizon, sa lumière traverse une plus grande couche d'air. Les composantes bleue, verte et jaune de la lumière sont de plus en plus diffusées et absorbées par des aéorosols, le soleil parait donc rouge.
2. Diffusion de Rayleigh
En 1871, John William Strutt Rayleigh fournit une
explication de la couleur du ciel en la reliant à la
diffusion de la lumière par les molécules d'air.
La diffusion de Rayleigh est la diffusion par les
molécules. Taille de la cible : 10
nanomètres. Lorsque la lumière traverse
l'atmosphère, elle est donc diffusée dans toutes
les
directions.
La taille de l'atome
est très faible devant la longueur d'onde de la radiation si
bien que les variations spatiales du champ
électromagnétique peuvent être
négligées à l'échelle du
nuage électronique. L'atome est alors soumis à la
force magnétique et la force électrique. La
première est négligeable devant la seconde.
D'autre part, le noyau étant beaucoup plus lourd que
l'électron, son déplacement est
négligé devant celui de l'électron.
On peut dessiner le comportement du nuage électronique
soumis à une radiation incidente :
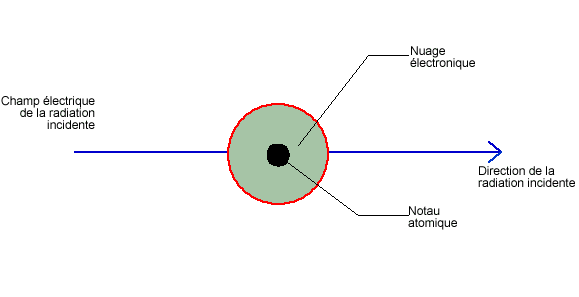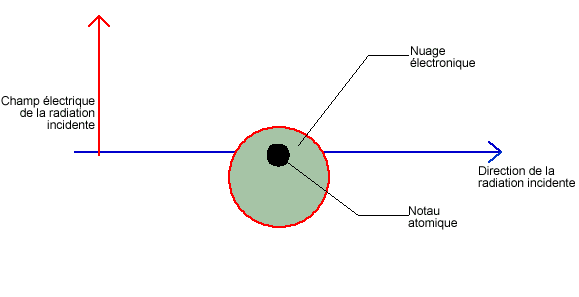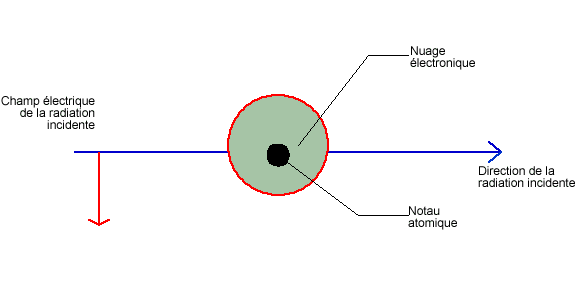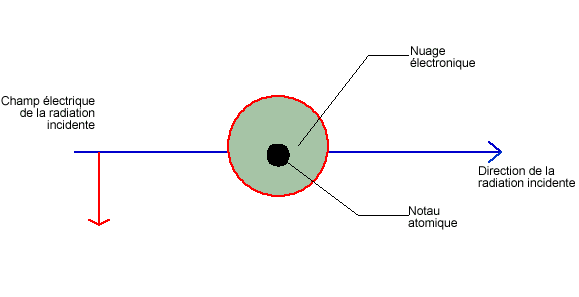
Schématisation
des oscillations du nuage électronique soumis à
une radiation incidente.
La distance noyau - barycentre (point d'équilibre) du nuage électronique
oscille
au cours du temps à la même pulsation que celle de
l'onde incidente.
La diffusion Rayleigh varie comme lambda à la puissance -4 (lambda étant la longueur d'onde). Elle est bien plus forte dans le bleu, à 400 nm, que dans le rouge à 650 nm. Ceci explique pourquoi le ciel est bleu la journée et le soleil rouge au couchant.
Sur l'image précédente, on voit que le bleu est bien plus diffusé que les autres longueurs d'onde.
3. Diffusion de Mie
La théorie de Mie, aussi appelée théorie de Lorenz-Mie, est une théorie de la diffraction de la lumière par des particules sphériques. Elle tire son nom du physicien danois Ludvig Lorenz et du physicien allemand Gustav Mie, qui lui donna sa première forme en 1908.La diffusion de Mie désigne la diffusion par des particules dont le rayon oscille entre 0.1 et 10 fois la longueur d'onde. Cette théorie est complexe et des résultats quantitatifs ne sont obtenus qu'avec des particules de géométries symétriques (ici sphériques). On note que la puissance diffusée est maximale lorsque la particule est grande devant la longueur d'onde.

Les propriétés de diffusion des particules dépendent de leur taille, de leur forme et de leurs constantes intrinsèques. Selon Mie, la quantité d'énergie diffusée vers l'avant est plus importante que dans n'importe quelle autre direction (voir figure). Lorsque la taille de la particule augmente, la diffusion vers l'avant augmente également. La diffusion type des particules plus importantes de la lumière incidente est illustrée par la figure ci-dessus.
Bien que la théorie de Mie soit compliquée, on peut trouver une relation simple entre la taille de la particule, la longueur d'onde et l'intensité.
La solution de Mie a été publiée il y a de nombreuses années. Etant donné qu'il n'y avait pas de solution analytique au problème, il a fallu attendre, pour son application, les progrès informatiques permettant le calcul numérique de nombreux coefficients et fonctions impliqués.
4. Confrontation des 2 théories
La diffusion de Rayleigh est un cas limite de la diffusion de Mie.
On peut apprécier la différence entre la
diffusion de Rayleigh et la diffusion de Mie en observant le ciel.
Les molécules qui constituent l'atmosphère explique la couleur bleue du ciel (Rayleigh).
La diffusion de Mie provient en partie des très fines
gouttelettes d'eau formant les nuages et expliquant leur couleur
blanche mais aussi des aérosols qui existent aux tailles
correspondant à cette diffusion.
La première diffusion est fortement dépendante de
la longueur d'onde, mais disperse uniformément dans toutes
les directions alors que la seconde varie faiblement avec la longueur d'onde.
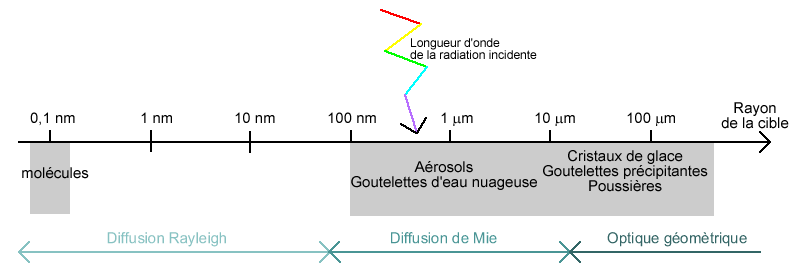
Lorsque la taille des particules cibles est très grande devant la longueur d'onde, les lois de l'optique géométrique sont applicables.
On étudie par exemple la diffusion à travers une goutte d'eau précipitant (menant par exemple à un arc en ciel) en appliquant les lois de Snells Descartes au passage de dioptres sphériques séparant l'air et l'eau, 2 milieux d'indices différents.

