En considérant le système décrit précédemment nous nous sommes aperçus que le champ magnétique était très difficilement calculable et nous n'y sommes pas parvenu malgré l'emploi d'outils performants comme le logiciel de calcul $Mathematica$. Cependant nous avons pu nous affranchir de cette difficulté en considérant un modèle simplifié et équivalent au système des deux plaques. Nous faisons donc quelques hypothèses pour faciliter les calculs et obtenir un champ magnétique équivalent à celui généré par les deux plaques:

• Une plaque peut être assimilée à un ensemble de câbles épais de diamètre égal à la hauteur des plaques. De cette manière la largeur de la plaque doit être un multiple entier de sa hauteur et on parlera de câbles liés aux plaques.
• Au centre des plaques le champ magnétique créé par les deux plaques est de même nature que celui créé par un système de câbles.
• Le courant électrique se répartit de manière uniforme dans chaque plaque, de cette manière chaque câble lié d'une même plaque possède la même densité volumique de courant. Un câble lié est donc parcouru par une intensité $I_c(t)$ égale à l'intensité totale $I(t)$ parcourant sa plaque divisé par le nombre de câbles.
• On suppose que le contact entre la bille et les plaques se fait de manière ponctuelle.
• On suppose, étant donné la taille des billes que nous considérons (moins de 5mm de diamètre), que le courant dans la bille est un courant linéaire qui passe par le plan équatorial de la bille d'une extrémité à l'autre de celle-ci.

Nous obtenons donc un système équivalent résumé par la représentation ci-dessous (dans cet exemple les plaques sont de largeur $4h$).

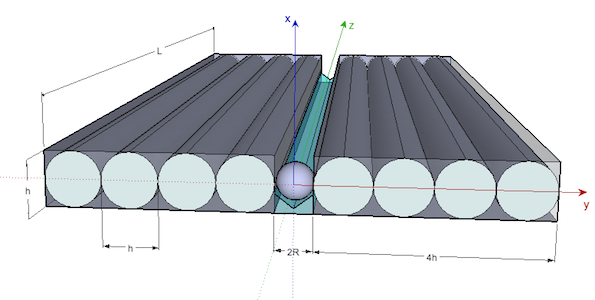
Représentation 3D du système

On appellera dans la suite la plaque de gauche la plaque 1 et la plaque de droite la plaque 2. Chaque câble d'une plaque sera couplé avec un câble de l'autre plaque (le symétrique par rapport au plan $xOz$ ). Les couples seront repérés dans les calculs par la lettre $n$ qui désignera l'ordre des câbles à partir de l'origine. Les câbles seront nommés câble $1_n$ (pour la plaque 1) et $2_n$ (pour la plaque 2). Ainsi le premier couple sera repéré par le numéro 1, le second par le numéro 2 et ainsi de suite.Les positions $b_1$ et $b_2$ du centre des câbles $1_n$ et $2_n$ suivant l'axe $Oy$ sont déterminées par: \[ \left\{ \begin{array}{r c l} b_1 &=& - R - (2n - 1)\frac{h}{2}\\ b_2 &=& R + (2n - 1)\frac{h}{2}\\ \end{array} \right. \] On considère trois points: deux points sources de champ magnétique $P_{1n}$ et $P_{2n}$ situés dans les câbles $1_n$ et $2_n$ ainsi qu'un point $M$ situé en dehors des plaques où on mesure le champ magnétique. Au vu des hypothèses établies dans la sous-section nous ne nous intéressons qu'au champ magnétique situé au niveau du centre de la bille. Les positions de ces points sont alors définies comme: \[ \left\{ \begin{array}{r c l} P_{1n} &:=& (0, b1, c)\\ P_{2n} &:=& (0, b2, c)\\ M &:=& (0, y, L(t))\\ \end{array} \right. \] Si notre bloc de condensateurs fournit un courant $I(t)$ le courant traversant un câble est $I_c(t) = I(t)/n$. On a alors, via la loi de Biot et Savart, le champ magnétique infinitésimal généré par une portion $dc$ des câbles $1_n$ et $2_n$ : $$\overrightarrow{dB} = \frac{\mu_0.I_c(t)}{4\pi}\left(\frac{ -\vec{dl} \wedge \overrightarrow{P_{1n}M} }{{P_{1n}M}^3}+ \frac{ \vec{dl} \wedge \overrightarrow{P_{2n}M} }{{P_{2n}M}^3}\right)$$ A noter que nous utilisons la perméabilité magnétique du vide puisque la perméabilité relative de l'aluminium vaut 1.000022, à l'échelle où nous travaillons et au vu des approximations et hypothèses que nous avons faites nous pouvons considérer que la perméabilité du vide et celle de l'aluminium sont égales. D'où en considérant que $\vec{dl} = \vec{ez}$ et en développant: $$\overrightarrow{dB} = \frac{\mu_0.I_c(t)}{4\pi}\left(\frac{(y - b_1) }{ {[(y-b_1)^2 + (L(t) - c)^2}]^{3/2}} -\frac{(y - b_2) }{ {[(y-b_2)^2 + (L(t) - c)^2}]^{3/2}}\right)dc. \vec{ex}$$ Il convient maintenant d'intégrer ce champ infinitésimal suivant $dc$ de 0 à $L(t)$ afin d'obtenir le champ magnétique total créé par le couple de câble $n$. On obtient alors: \begin{equation}\overrightarrow{B} = \frac{\mu_0.I_c(t).L(t)}{4\pi}\left(\frac{1}{(y - b_1)\sqrt{(y - b_1)^2 + {L(t)}^2}} - \frac{1}{(y - b_2)\sqrt{(y - b_2)^2 + {L(t)}^2}}\right)\vec{ex}\end{equation}