Méthode des dérivées
Il existe une méthode basée sur la théorie des transferts de rayonnement en lumière polarisée qui nous donne dans l’approximation des champs faibles les expressions des paramètres de Stokes :
Comme nous pouvons le voir, ces relations sont directement liées au champ magnétique compte tenu de l'équation [1] et en remplaçant tout en utilisant les notations adéquates, nous obtenons :
V(λ) permet donc de trouver le champ longitudinal tandis que Q(λ) et U(λ) permettent de trouver le champ transversal ainsi que l’azimut ϕ.
Remarque : le profil V(λ) est proportionnel à la dérivée première de I par rapport à λ.
Résultats obtenus via cette méthode
Traçons alors la dérivée première de I par rapport à λ en fonction de λ. Nous obtenons :
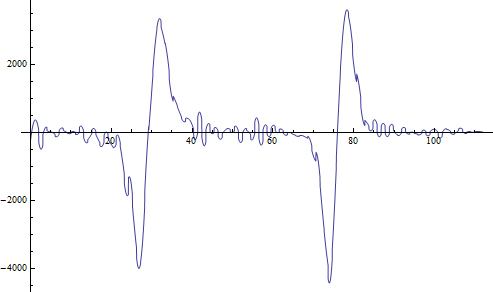
Et comparons alors cette courbe au spectre de V ci dessous prise au pixel arbitraire (100,400) sachant qu'au total il y a 190x816 pixels :

On ne remarque pas de similitudes avec le graphe précedent, cependant si l'on regarde sur un plus grand nombre de pixels en même temps on obtient :

On observe que malgré le bruit omniprésent, certains pixels se démarquent et l'on peut y observer les mêmes motifs que sur la dérivée de I par rapport à λ.
Toutefois, le rapport bruit/signal étant présent de façon trop aléatoire dans nos données, il nous est impossible d'exploiter quoique ce soit.
De plus, étant donné que nous regardons au centre du Soleil (bloc d'image 7 sur 14), l'angle θ est égal à 0 et par conséquent, Q et U sont nuls (nous n'obtenons que du bruit dans ces 2 spectres)
Méthode du centre de gravité
Le principal problème de la méthode précédente, était qu'elle dépendait trop du rapport bruit/signal.
Avec cette méthode du centre de gravité on arrive à se débarasser du bruit, de façon notable. Pour cela nous allons effectuer une intégrale sur toute la largeur d'une des deux raies.
Nous allons choisir la raie 2 étant donné qu'elle dispose d'un plus grand facteur de landé. Pour rappel on a glraie 1 = 1,67 et glraie 2 = 2,5 ce qui indique que la raie 2 est plus sensible au champ magnétique.
λ± correspond à la valeur de λ au centre des creux des profils respectifs I+V et I-V, espacés de la valeur 2∆λB, voir schéma sur l'écart Zeeman.
Ic est l’intensité dans le continu que l’on calcule aisément en faisant une moyenne des valeurs hors des raies. On a Ic = 21 500.
Résultats obtenus via cette méthode
Grâce au logiciel Mathematica, on obtient les valeurs suivantes:
Moyenne : 5,8 Gauss (en comptant les champs négatifs et positifs).
Minimum : -1641.31 Gauss.
Maximum : 7916.15 Gauss.
Remarque : 50 Gauss correspond à l’intensité du champ magnétique d’un aimant sur un réfrigérateur : source.
Afin d'avoir des valeurs plus représentatives nous prenons la valeur absolue :
Moyenne : 15.7 Gauss
On voit ici que les champs sont en général très faible, et c'est bien ce à quoi nous nous attendions. Traçons maintenant l'histogramme des valeurs :
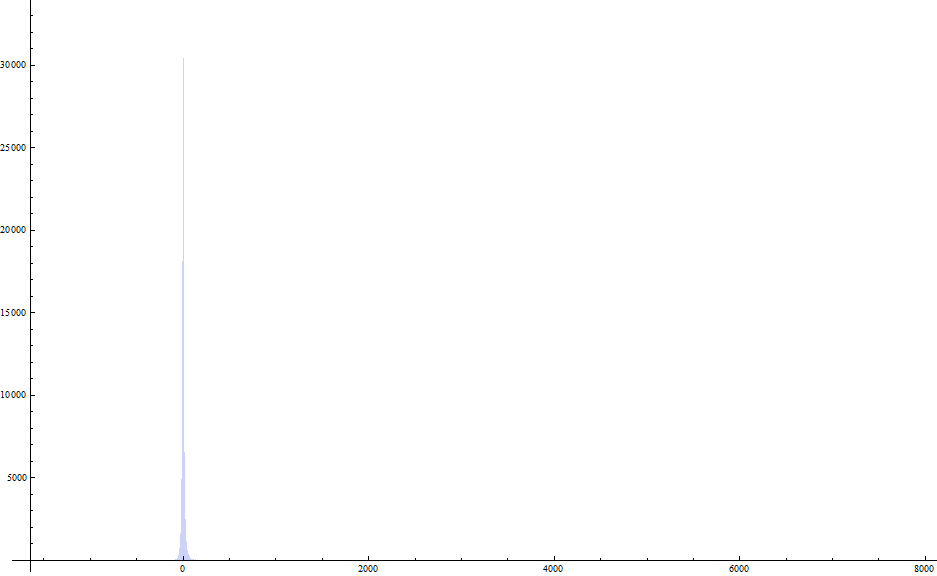
Cet histogramme montre bien la répartition des champs magnétiques. Traçons maintenant cet histogramme en échelle logarithmique afin de mieux observer la dynamique du système :
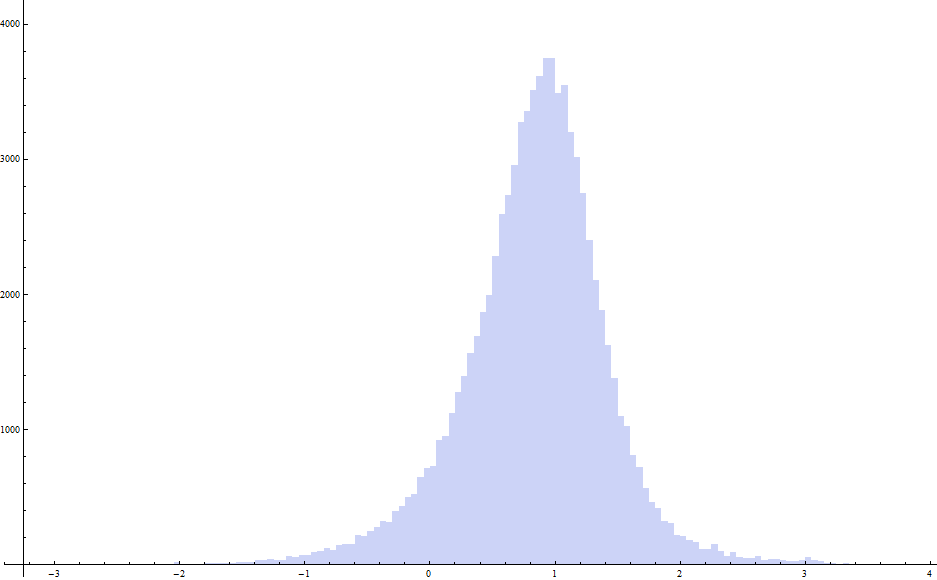
Et enfin voyons maintenant la cartographie du champ magnétique solaire :


