Étude des champs magnétiques dans les régions calmes du Soleil

Satellite Hinode

Hinode est un satellite, lancé le 23 septembre 2006 depuis le Uchinoura Space Center au Japon. Sa mission est consacrée à l'observation du Soleil. Pour cela il dispose de 3 instruments, mais nous allons nous intéresser qu'à l'un d'entre eux : le SOT (Solar Optical Telescope).
Pour mener à bien notre étude nous disposons de données de polarisations issues d’un polarimètre. À l'origine, toutes nos données sont au format .FITS et seront lues grâce au logiciel Wolfram Mathematica.

Fente

Voyons maintenant comment procède Hinode afin de récolter ses données.
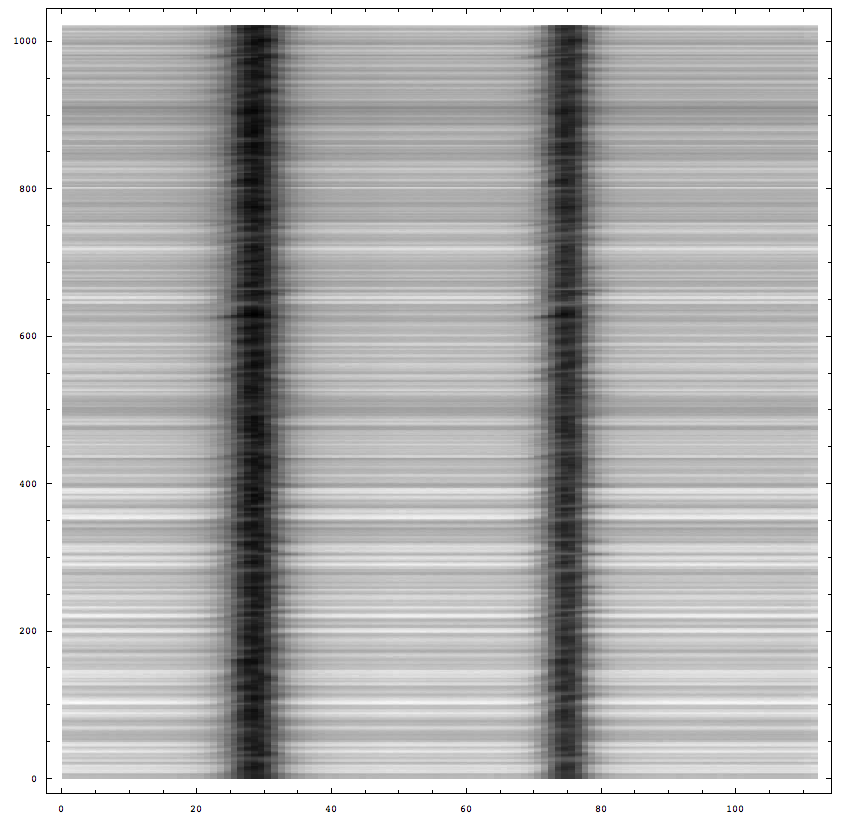
Il va répartir l’axe Nord-Sud du Soleil en vingt zones qui seront « scannées ». Dans chacune de ces vingt zones, il va déplacer une fente sur 380 positions Est-Ouest, et cette fente fera 1024 pixels de hauteur. De plus, il effectuera aussi un balayage en longueur d’onde de 112 unités.

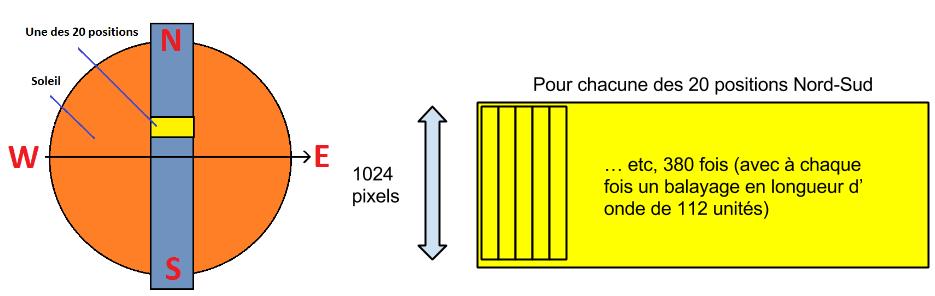
Au final, au niveau des données, nous disposerons donc de 20 dossiers correspondants au 20 blocs Nord-Sud. Et dans chaque dossier nous aurons 380 fichiers correspondants aux positions Est-Ouest. On dit que l’on obtient : « des cubes de données »

NB : Dans nos données, nous disposons d’en fait 14 blocs Nord-Sud, et la fente ne fait que 816 pixels de hauteur et n’effectue un balayage Est-Ouest que sur 190 positions, du fait de l’usure de l’appareil.

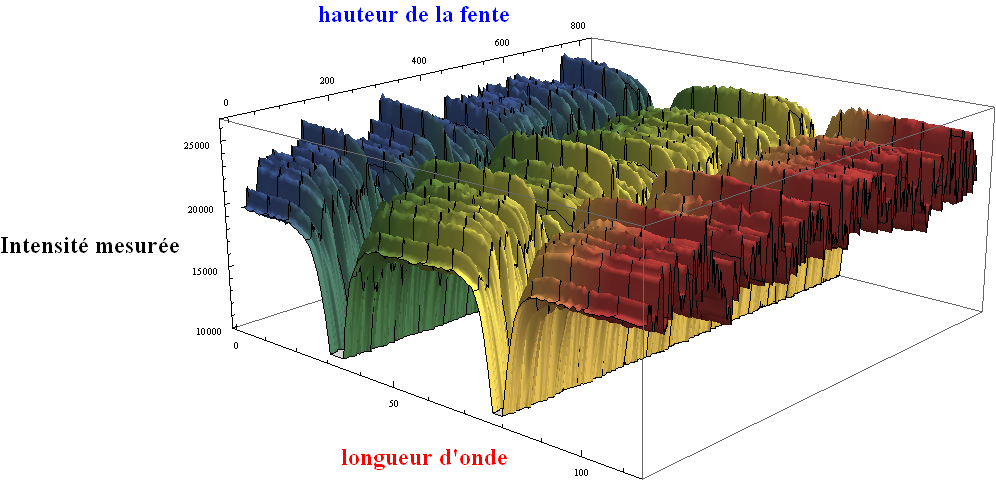
Dans l’optique d’étudier les champs magnétiques, le polarimètre se restreint à une gamme de longueur d’onde de l’atome de Fer car cet élément est sensible au champ magnétique. En termes physiques, on dit que le Fer dispose d’un grand facteur de Landé.
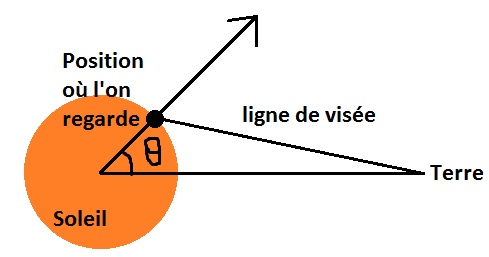
Introduisons aussi la notion de ligne de visée et de l’angle θ, qui nous serviront par la suite :

Les unités de Hinode

Nous pouvons voir dans les différents graphes du dessus, que les unités ne font pas parties des unités standards.
De plus nous avons la relation 0,16'' = 114 km sur le Soleil (au mois de Décembre).
Au final 1 pixel = 114 km = 0,16''.
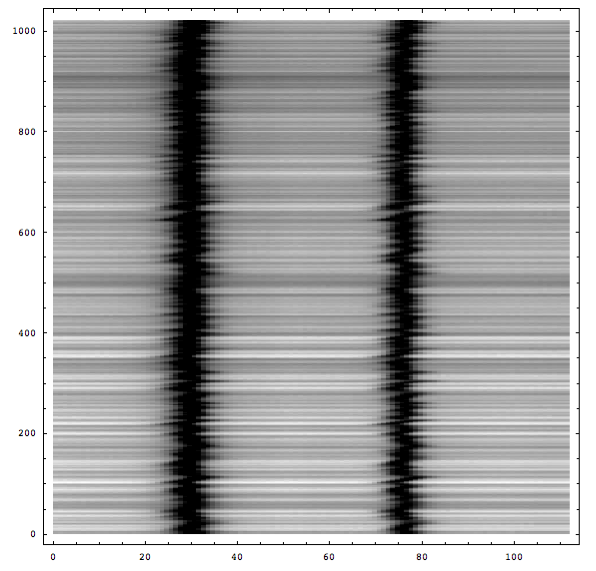
En ce qui concerne les longueurs d'ondes, nous savons que ce sont 2 raies du Fer, séparées par Effet Zeeman, et ces longueurs d'ondes sont connues : 630,15 nm pour la raie Fe1 et 630,25 nm pour la raie Fe2.
Par la suite, ce qui sera important, sera surtout l'écart entre les raies.

Facteur de Landé

Le facteur de Landé est une grandeur physique sans dimension qui, globalement, relie le moment cinétique et le moment magnétique d'un atome.
Dans notre projet il nous servira principalement à déterminer les composantes qui sont les plus sensibles au champ magnétique.
Un plus grand facteur de Landé indique une plus grande sensibilité à un champ magnétique. On le notera g_l.

Traitement des images

Lors de l’acquisition des données par le satellite, l’instrument va mettre un certain temps à déplacer la fente sur l’axe Est-Ouest. Cependant le Soleil n’étant pas une sphère inerte, il y aura des différences notables entre deux positions de fentes. La principale cause à prendre en compte, sont les mouvements de convection au sein du Soleil. Il y a en permanence du plasma qui circule en remontant vers la surface puis ensuite qui redescend. Ce mouvement du plasma de bas en haut puis de haut en bas, va induire un effet bien connu : l’effet Doppler. Vu du télescope, le plasma va se rapprocher ou s’éloigner. L’effet Doppler aura pour conséquence de décaler les profils de raies en longueur d’onde. Il faudra donc corriger cet effet afin d’aligner les raies d’absorption entre différentes positions de la fente.
Pour se faire, on prend un emplacement arbitraire sur lequel on va centrer les raies des autres positions. On passe dans l’espace de Fourier et on multiplie la position en longueur d’onde par une exponentielle complexe appropriée, puis on repasse dans l’espace direct.

Ce traitement aura pour effet de translater les raies afin de les aligner toutes au même endroit.
Considérant la complexité de ce traitement au niveau de la pogrammation Mathematica, les codes sources nous ont été fournis.
On appelera ces données : données droitisées.

Dispositif de lames à retard

Afin d'expliquer le fonctionnement de ce dispositif considérons un dispositif constitué de deux lames à retard L₁,L₂ et d’un polariseur P tous orthogonaux a l’axe (O_z) . Étudions l'effet de ce dispositif sur une onde électrommagnétique se propageant selon l'axe (O_z) dans le sens des z croissants.

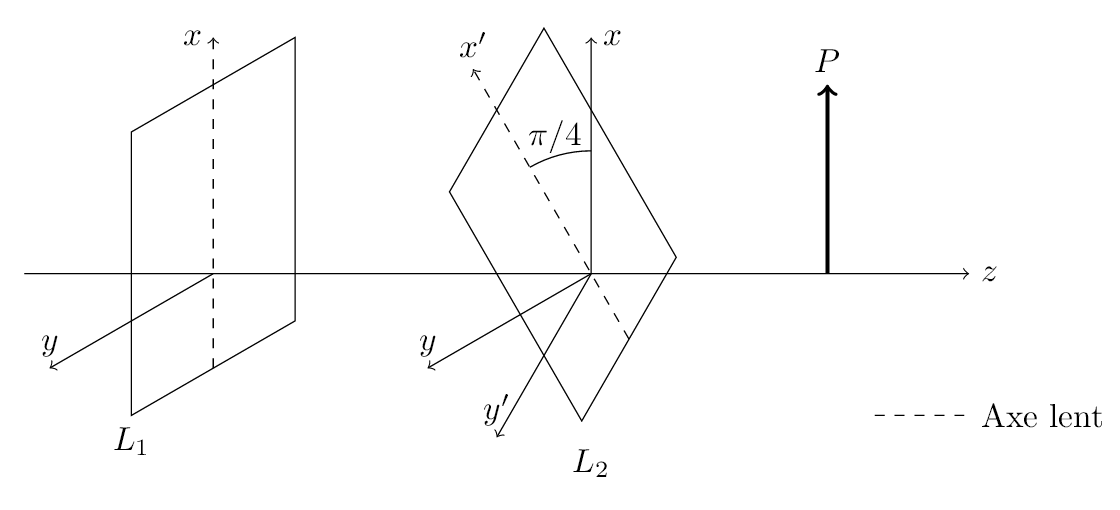
Les lames L₁ (respectivement L₂ ) possèdent chacune un axe lent et un axe rapide. Par conséquent la propagation de la composante du champ éléctrique colinéaire à l'axe lent aura un retard de phase φ₁ (respectivement φ₂) par rapport a l'axe rapide.
Nous pouvons montrer que l'intensité en sortie du polariseur peut s'écrire :

Pour différents couples (φ₁,φ₂) on obtient:

Ainsi nous voyons qu'il est possible en théorie de jouer avec les angles φ₁ et φ₂ afin d'obtenir des "couples" de polarisation.

B et la ligne de visée

Nous allons maintenant définir ce que sont B_┴ et B_// grâce à ce schéma :

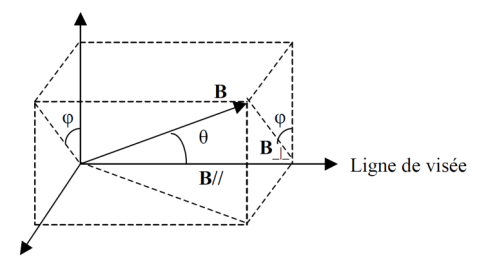
Nous avons les relations :

• Champ longitudinal: B_// = B cos(θ)
• Champ transversal: B_┴ = B sin(θ)

Ces notations nous seront grandement utiles par la suite.