Tomographie
Nous souhaitons vérifier que notre source émet des photons dans l'état souhaité. Pour cela, il faut reconstruire son opérateur densité en effectuant une tomographie. Nous pouvons alors déterminer si notre source est une source pure ou si elle génère une mixture statistique.
Reconstruction de l’opérateur densité
Il est toujours possible de décomposer l'opérateur densité d'un système mono-partite de la façon suivante:
$$\hat{\rho}= \frac{1}{2} \sum_{i=0}^{3}S_{i}\sigma_{i}$$
Avec $S_{i}$ les paramètres de Stokes et $\sigma_{i}$ les matrices de Pauli
Les paramètres de Stokes se décomposent comme:
$$ S_{0} = P_{|{H}\rangle}+P_{|{V}\rangle} $$
$$ S_{1} = P_{ \frac{1}{ \sqrt{2} } (|{H}\rangle + |{V}\rangle)}-P_{\frac{1}{ \sqrt{2} } (|{H}\rangle - |{V}\rangle)} $$
$$ S_{2} = P_{ \frac{1}{ \sqrt{2} } (|{H}\rangle + i|{V}\rangle)}-P_{\frac{1}{ \sqrt{2} } (|{H}\rangle -i|{V}\rangle)}$$
$$ S_{3} = P_{|{H}\rangle}-P_{|{V}\rangle} $$
où $ P_{|{ \psi }\rangle} $ est la probabilité de trouver le système dans l'état $|{ \psi }\rangle$ lorsqu' on effectue une mesure projective sur ce dernier.
Pour un système bipartite, la décomposition de l'opérateur densité s'effectue ainsi:
$$\hat{\rho}=\dfrac{1}{4}\sum_{i,j=0}^{3}S_{ij}\sigma_{i}\sigma_{j}$$
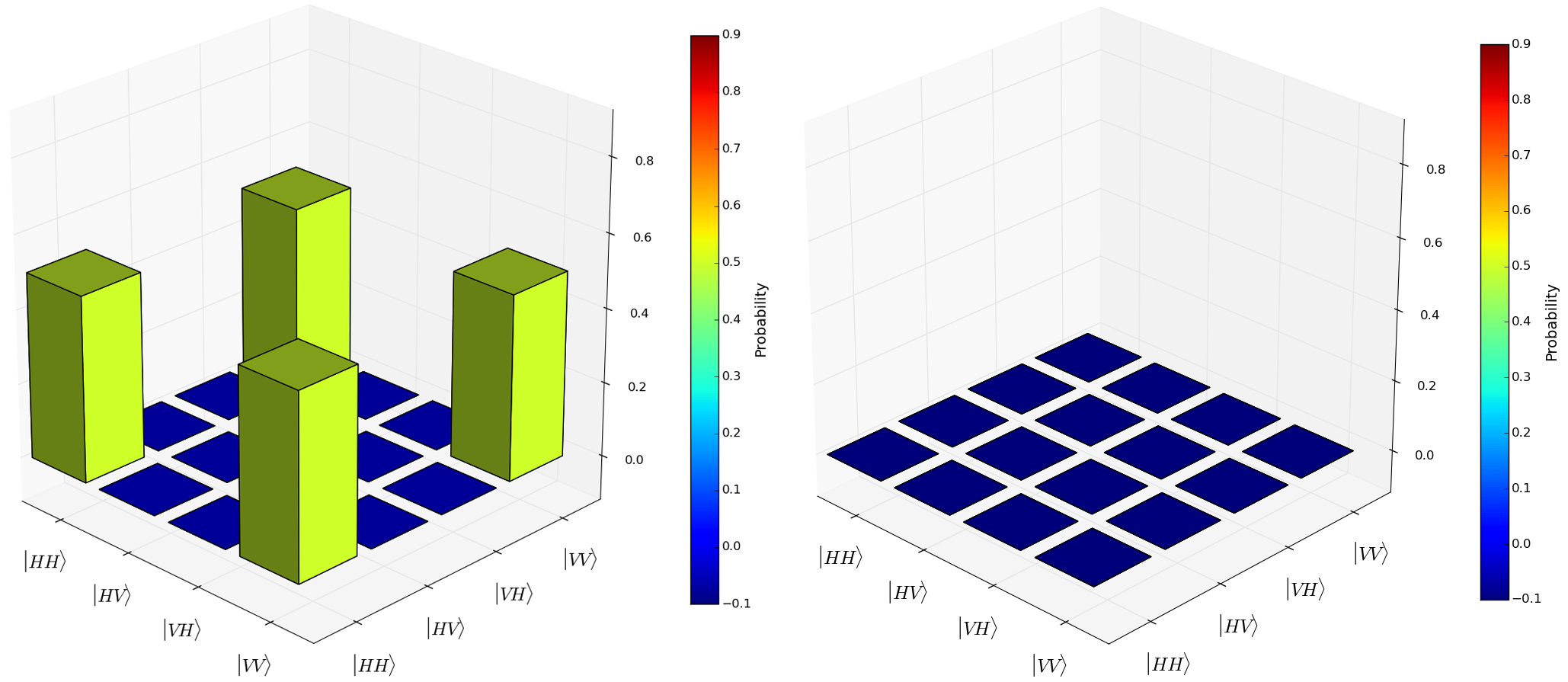
En pratique pour retrouver les paramètres de Stokes, il suffit donc de connaître les différentes probabilités de trouver le système dans l'état $|{\psi}\rangle$.A titre d'exemple, voici l'opérateur densité associé l'état de Bell $|{\Phi}_{+}\rangle$ (à gauche partie réelle et à droite partie imaginaire).
Diapositif expérimental permettant de réaliser la tomographie
Pour remonter expérimentalement aux différents $P_{|{\psi}\rangle}$, nous avons ajouté trois éléments optiques: une lame demi-onde, une lame quart-d'onde et un polariseur. Afin de projeter l'état de polarisation incident sur une direction de polarisation donnée, nous avons fait le choix de prendre un point de vue actif. Le système de projection que constitue le polariseur restera orienté pour l'ensemble des mesures selon une direction donnée que nous avons pris comme la direction verticale, et c'est la lumière incidente qui est alors manipulée en utilisant l'action successive de la lame demie-onde et de la lame quart-d'onde. La lame demie-onde permet d'orienter la projection selon une direction contenue entre $|{V}\rangle$ et $|{H}\rangle$, alors que la lame quart-d'onde permet quant à elle d'ajouter une composante complexe qui sert à venir projeter le système selon les directions de polarisation circulaire gauche et circulaire droite (respectivement notées $|{L}\rangle$ et $|{R}\rangle$).
Afin de décrire mathématiquement l'action successive des divers éléments d'optique, il est d'usage d'avoir recours au formalisme de Jones. Avec ce formalisme, les états de polarisation se décrivent comme: $$|{V}\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}, |{H}\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$$ et les transformations effectuées sur le faisceau incident par les lames demi-onde et quart-d'onde sont décrites par les opérateurs: $$\hat{U}_{QWP}=\frac{1}{\sqrt{2}}\begin{pmatrix} i-cos(2q) & sin(2q) \\ sin(2q) & i+cos(2q) \end{pmatrix}$$ $$\hat{U}_{HWP}=\begin{pmatrix} cos(2h) & -sin(2h) \\ -sin(2h) & -cos(2h) \end{pmatrix}$$ L'action successive d'une lame demie-onde et d'une lame quart-d'onde sur un état de polarisation verticale se décrit alors ainsi : $$\begin{eqnarray} |{\psi_{proj}(h,q)}\rangle&=&\hat{U}_{QWP}(q)\cdot\hat{U}_{HWP}(h)\cdot\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &=&a(h,q)|{H}\rangle+b(h,q)|{V}\rangle \end{eqnarray}$$ avec a(h,q) et b(h,q) données par : $$a(h,q)=\frac{1}{\sqrt{2}}\{sin(2h)-i sin(2(h-q))\}$$ $$b(h,q)=-\frac{1}{\sqrt{2}}\{cos(2h)+i cos(2(h-q))\}$$ La description qui vient d'être donnée se généralise immédiatement au cas d'un système bipartite : $$|{\psi_{proj}(h_{1},q_{1},h_{2},q_{2})}\rangle=|{\psi_{proj}(h_{1},q_{1})}\rangle\otimes|{\psi_{proj}(h_{2},q_{2})}\rangle$$ Un choix adéquat d'angles h1; q1; h2; q2 permettra alors de venir projeter l'état incident sur n'importe quelle direction souhaitée.
Les différents $P_{|{\psi}\rangle}$ i s'obtiennent alors en normalisant le nombre de coïncidences obtenues pour le choix d'angles correspondant par la somme de l'ensemble des coïncidences obtenues dans les différentes configurations.
| $\nu$ | Mode 1 | Mode 2 | $h_{1}$ | $q_{1}$ | $h_{2}$ | $q_{2}$ |
|---|---|---|---|---|---|---|
| 1 | $|{H}\rangle$ | $|{H}\rangle$ | 45° | 0 | 45° | 0 |
| 2 | $|{H}\rangle$ | $|{V}\rangle$ | 45° | 0 | 0 | 0 |
| 3 | $|{V}\rangle$ | $|{V}\rangle$ | 0 | 0 | 0 | 0 |
| 4 | $|{V}\rangle$ | $|{H}\rangle$ | 0 | 0 | 45° | 0 |
| 5 | $|{R}\rangle$ | $|{H}\rangle$ | 22.5° | 0 | 45° | 0 |
| 6 | $|{R}\rangle$ | $|{V}\rangle$ | 22.5° | 0 | 0 | 0 |
| 7 | $|{D}\rangle$ | $|{V}\rangle$ | 22.5° | 45° | 0 | 0 |
| 8 | $|{D}\rangle$ | $|{H}\rangle$ | 22.5° | 45° | 45° | 0 |
| 9 | $|{D}\rangle$ | $|{R}\rangle$ | 22.5° | 45° | 22.5° | 0 |
| 10 | $|{D}\rangle$ | $|{D}\rangle$ | 22.5° | 45° | 22.5° | 45° |
| 11 | $|{R}\rangle$ | $|{D}\rangle$ | 22.5° | 0 | 22.5° | 45° |
| 12 | $|{H}\rangle$ | $|{D}\rangle$ | 45° | 0 | 22.5° | 45° |
| 13 | $|{V}\rangle$ | $|{D}\rangle$ | 0 | 0 | 22.5° | 45° |
| 14 | $|{V}\rangle$ | $|{L}\rangle$ | 0 | 0 | 22.5° | 90° |
| 15 | $|{H}\rangle$ | $|{L}\rangle$ | 45° | 0 | 22.5° | 90° |
| 16 | $|{R}\rangle$ | $|{L}\rangle$ | 22.5° | 0 | 22.5° | 90° |
Configuration des lames demie-onde et quart-d'onde pour les differentes projections necessaires à la reconstruction de l'opérateur densité du système. Avec: $|{D}\rangle=(|{H}\rangle+|{V}\rangle)/\sqrt{2}, |{L}\rangle=|{H}\rangle+i|{H}\rangle)/\sqrt{2}, |{R}\rangle=|{H}\rangle-i|{H}\rangle)/\sqrt{2}$
A titre d'exemple, $P_{|{HH}\rangle}$ s'obtiendront ainsi: $$P_{|{HH}\rangle} = \frac{ C_{HH} }{C_{HH} + C_{HV} +C_{VH} + C_{VV}}$$ avec $C_{ij}$ le nombre de coincidences obtenus dans la configuration ij.