Avant de rentrer directement dans le vif du sujet, il est nécessaire de poser les bases des notions liées à la topologie. Il y a notamment deux aspects important : la notion de propriété globale et la notion de propriété locale.

La notion de globalité

On l'a vu en introduction, et c'est généralement comme cela que la topologie est introduite, que cette dernière permet de décrire les objets dans leur globalité, et de montrer que ceux-ci restent équivalent malgré des transformations continues. L'équivalence en topologie "géométrique" est caractérisée par un trou, que l'on appelle invariant topologique ou encore le genre $\nu$. Un ballon de football restera équivalent à un ballon de rugby et à tout objet ne possédant pas de trou. Bien que les propriétés locales soient très différentes, et on le remarque avec un le ballon de rugby, qui à l'inverse du ballon de football, a des courbures différentes entres ses pôles ; ces deux objets appartiennent bel et bien à une même classe topologique, gouvernée par un genre équivalent, ainsi la propriété globale reste la même pour chaque classe topologique.

Notion de propriété locale et phase de Berry

Même si on vient d'affirmer que les propriétés locales ne jouaient pas (à priori) un rôle en topologie, les prendre en considération est primordiale pour la suite. Pour pouvoir bien assimiler ce qui va suivre, nous allons commencer par présenter un phénomène lié à la géométrie pour ensuite pouvoir comprendre son analogue en mécanique quantique [7].

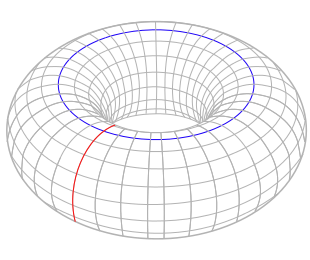
Ce phénomène géométrique, c'est le transport parallèle. Le transport parallèle est un moyen "transporter" les informations géométriques (d'un vecteur par exemple) le long d'une courbure locale sur un espace courbé (que l'on appelle variété, cela peut être un espace Euclidien en géométrie, ou un espace de Hilbert en quantique). Si on choisit une sphère comme espace courbé et une courbure locale fermée comme sur l'illustration ci-dessous, et que l'on choisit un vecteur tangent comme porteur d'informations, on s'aperçoit que lorsque l'on effectue un tour complet le long de la trajectoire fermée, on observe un décalage d'angle entre le vecteur initial et le vecteur final. On appelle ce décalage d'angle une holonomie.

Exemple d'un transport parallèle sur une sphère

On peut donc faire le rapprochement du transport parallèle en changeant les "paramètres" pour notre approche de la mécanique quantique. La variété caractérise maintenant un espace de Hilbert courbé, et le vecteur géométrique est remplacé par une fonction d'onde (un ket). On observe le même phénomène lorsque cette fonction d'onde suit un chemin fermé, et l'holonomie ici ressort d'un changement de phase.

Cette phase est appelée la phase de Berry. Mise en avant par Michael Berry c'est néanmoins Barry Simon qui a réalisé que celle-ci était en fait l'équivalent d'une holonomie et s'écrit $\mathcal{A} = \langle\psi |\vec{\nabla}\psi\rangle \cdot \vec{dl}$

Le lien entre les propriétés locale et globale et nombre de Chern

Le théorème de Gauss-Bonnet

Il existe en topologie un théorème particulièrement remarquable qui relie la propriété globale d'un objet à ses propriétés locales : c'est le théorème de Gauss-Bonnet, se présentant sous la forme suivante : $\frac{1}{2\pi}\int_{\Sigma} \mathcal{F} \mathrm{d}S = 2(1 - \nu)$ Le terme de gauche décrit les propriétés locales de l'objet, et n'est pas forcément quantifié, avec $\Sigma$ la surface totale de l'objet et $\mathcal{F}$ se courbure locale intégrée sur un élément $\mathrm{d}S$.
Le terme de droite de son côté ne dépend que du genre $\nu$ introduit précédemment. On remarque donc très bien d'après ce théorème que l'intégrale de la courbe gaussienne sur toute la surface, et ce, quelque soit la forme de l'objet, est donnée par le genre. Si on change arbitrairement $\mathcal{F}$ d'une sphère par exemple en ajoutant des courbures particulières ou en augmentant la surface totale en l'étirant, le terme de droite piloté par le genre, reste le même.

Le nombre de Chern

Le théorème de Gauss-Bonnet se généralise sous la forme appelée théorème de Gauss-Bonnet-Chern s'écrivant $\frac{i}{2\pi} \int_{\mathcal{M}} \mathcal{F} = \mathcal{C}$ Où sous cette forme, l'intégrale correspond à la courbure de Berry et $\mathcal{C}$ est appelé nombre de Chern.

L'approche par les réseaux périodiques

Dans la partie précédente, nous avons montré que le spectre de Landau était continu et que l'effet Hall quantique était robuste au désordre notamment. Cette notion de robustesse est un élément important pour pouvoir avoir une approche topologique. En effet, les variations de la température, du désordre et d'autres détails microscopiques ne modifiaient pas la conductance globale. Et c'est à partir de ce constat qu'en 1982, Thouless, Kohmoto, Nightingale et Nijs (TKNN), on pu passer par une analogie aux réseaux périodiques.

Potentiels périodiques et théorème de Bloch

Dans le cas d'un système où les propriétés du milieu varient périodiquement dans l'espace, on peut écrire l'Hamiltonien correspondant sous la forme $H = H_0 + V(\vec{r})$ avec $V(\vec{r} + \vec{R}) = V(\vec{r})$ où $\vec{R}$ est le vecteur unitaire du réseau de Bravais, constitué de vecteurs élémentaires de la forme $\vec{R} = n\vec{a} + m\vec{b} + l\vec{c}$ à trois dimensions, avec $\vec{a}$, $\vec{b}$ et $\vec{c}$ les vecteurs élémentaires du réseau.

Pour construire un réseau périodique, trois ingrédients sont nécessaire, on a besoin :

• du motif de la maille élémentaire, c'est à dire du nombre d'atome par maille,
• de placer une origine arbitraire,
• et de fixer les vecteurs élémentaires de Bravais.

Le théorème de Bloch permet de trouver les fonctions d'onde qui sont les états propres de l'Hamiltonien d'un système présentant un potentiel périodique, et sont de la forme $\psi(\vec{r}) = e^{i\vec{k}\cdot\vec{r}} u_{\vec{k}}(\vec{r})$ avec $u_{\vec{k}}(\vec{r})$ qui admet la périodicité que le potentiel, et $ u_{\vec{k}}(\vec{r} + \vec{R}) = u_{\vec{k}}(\vec{r})$, ainsi, si l'on déplace la fonction proportionnellement à la période du réseau, la phase de la fonction d'onde change telle que $\psi(\vec{r} + \vec{R}) = e^{i\vec{k}\cdot\vec{R}}\psi(\vec{r})$ En deux dimensions, pour une périodicité $a$ suivant $\vec{e_x}$ et une périodicité $b$ suivant $\vec{e_y}$, le vecteur d'onde de Bloch est de la forme $\vec{k} = \frac{2\pi}{a}\vec{e_x} + \frac{2\pi}{b}\vec{e_y}$ Ainsi, on peut en déduire la première zone de Brillouin telle que $k_x \in \left[-\frac{\pi}{a}, \frac{\pi}{a}\right] \quad \text{ et } \quad k_y \in \left[-\frac{\pi}{b}, \frac{\pi}{b}\right]$

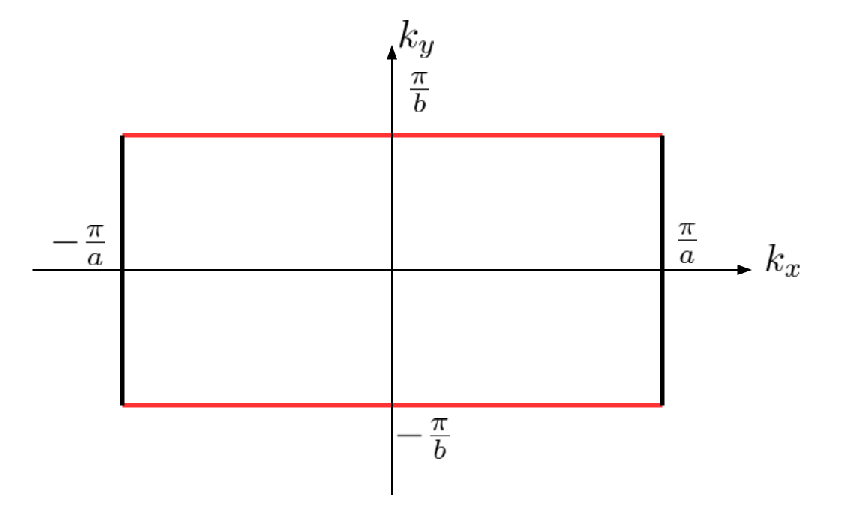Première zone de Brillouin

On a donc la zone de Brillouin définie dans l'espace réciproque que l'on peut transformer en un tore $T^2$ par "recollement" grâce aux conditions de périodicité du réseau.

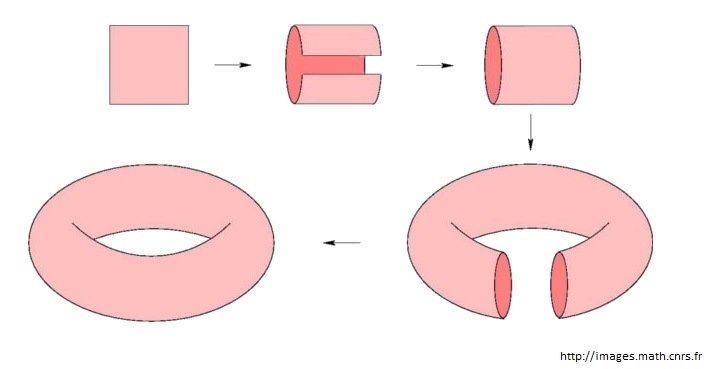Construction d'un tore

À partir de ces considérations, TKNN ont pu fournir une expression précise de la conductivité transverse, et le nombre d'états sur un niveau $\alpha$ de Landau est donné par $N(E_{\alpha}) = \frac{i}{2\pi}\int_{T^2} (\langle\frac{\partial\psi}{\partial k_x}|\frac{\partial\psi}{\partial k_y}\rangle - \langle\frac{\partial\psi}{\partial k_y}|\frac{\partial\psi}{\partial k_y}\rangle) dk_x dk_y$ On remarque la grande ressemblance avec la phase de Berry, et Barry Simon en 1983 relie l'équation de TKNN au nombre de Chern par la formule de Gauss-Bonnet généralisé et au nombre de Chern prenant une valeur entière. L'intégrale ici s'effectue sur toute la zone de Brillouin et TKNN sont retombé à partir de la conductance de Hall à l'expression de la résistance de Hall : $R_H = \frac{h}{\mathcal{C}e^2}$

Cette approche topologique permet de retrouver le même résultat que nous donnais l'approche par les niveaux de Landau. On comprend aussi ici plus facilement par les arguments de la topologie que la résistance reste quantifiée malgré certaines perturbations locales.

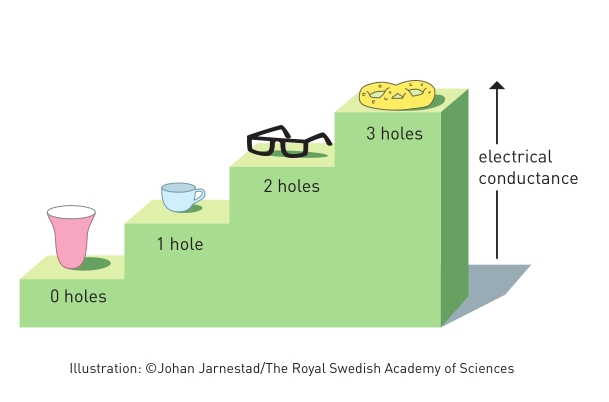Relation entre la conductance et la topologie géométrique