La topologie est une branche des mathématique qui a éclot de l'étude de la géométrie, mais en s'en séparant rapidement pour en étudier les propriétés de l'espace sans se soucier des notions de "grandeur" (distances entre points par exemple). Une manière commune d'introduire la topologie est de montrer qu'il est possible de déformer une tasse de café en un bagel (donut) de manière continue sans effectuer de découpage ni de collage. Le nombre de trous peut donc être assimilé à un invariant topologique, qui peut être utilisé pour grouper les objets en différentes classes.

Déformation continue d'une tasse de café en bagel

Bien que la topologie est souvent introduite de manière à s'en faire une idée très visuelle où en géométrie elle est définie par un invariant comptant le nombre de trou, en dépit de la forme de l'objet, il faut savoir qu'en physique l'utilisation de la topologie ne s'effectue pas au niveau du matériau "physique" en lui même ni à sa forme, mais au niveau de sa structure de bande du spectre d'énergie. La topologie offre une robustesse et donc des protections contre les imperfections encourageant des fascinantes possibilités d'applications.

Longtemps les physiciens n'ont pas cru en la topologie comme un outil mathématique utile à leurs travaux, elle est désormais présente dans énormément de domaines, couvrant la physique de la matière condensée à la cosmologie en passant par la photonique.
Sans en couvrir toutes les subtilités et sans entrer dans les détails mathématiques, voici quelques domaines de la physique où la topologie se manifeste de plus en plus pour proposer des solutions à des problèmes portant pour certains des applications pour un futur plus ou moins proche.

La topologie au sommet de la physique en 2016

En 2016, l'Académie Royale des Sciences de Suède décide de décerner le Prix Nobel de physique à trois physiciens théoriciens britanniques, David J. Thouless, F. Duncan M. Haldane et J. Michael Kosterlitz pour leur "découvertes théoriques des transitions de phases topologiques et des phases topologiques de la matière" [2]. Deux informations essentielles en ressortent : la notion de transition de phase topologique et phases topologiques de la matière.

Duncan Haldane, Micheal Kosterlitz et David Thouless

La première fait référence aux travaux dans les années 70 de Kosterlitz et Thouless, chercheurs éponymes de la transition $KT$, et la seconde est la description topologique de l'effet Hall quantique, porté par Thouless et Haldane que nous verrons largement en détails dans les parties suivantes. La transition de phase $KT$ est largement présentée en première partie du rapport avec notamment la mise en avant de l'importance des symétries.
La transition $KT$ s'effectue dans ce qu'on appelle un phase exotique de la matière, c'est à dire à très basses températures et en deux dimensions, où les transitions de phases étaient supposées impossibles. La force de cette nouvelle transition de phase de nature topologique est qu'elle est universelle pouvant être appliquée à différents types de matériaux et a ainsi permis d'expliquer des expériences avec plusieurs différents types de systèmes physiques, comme par exemples les films d'Hélium 4, ou des rubans supraconducteurs...

Les autres domaines en physique

Si la topologie connais un élan considérable depuis une dizaine d'années, elle était toute fois beaucoup utilisée que ce soit en physique quantique ou relativiste. C'est à partir de considérations topologiques que Paul Dirac à montré l'existence possible de monopoles magnétiques. La physique des hautes énergies, le modèle standard et la cosmologie se servent tout autant de la topologie.

En photonique, où pourtant les systèmes optiques sont très sensibles au désordre et autres impuretés, on est désormais en mesure de créer des appareils capables d'exploiter ces états très robustes qu'offre la topologie afin de guider la lumière. De manière similaire, les mêmes principes peuvent être appliqué en mécanique où l'on peut, à partir de ces idées, guider et contrôler des ondes acoustiques (ou autres ondes mécaniques) à travers un matériau. La découverte récente des isolants topologiques ayant la particularité d'être isolant en volume mais conducteur en surface porte notamment l'espoir d'ordinateurs quantiques.

La topologie en dehors de la physique

Si l'Académie de Sciences de Suède à décerné le prix Nobel de physique faisant la part belle de la topologie, cette dernière est aussi présente dans le prix Nobel de chimie [3]. En effet, les machines moléculaires de Jean-Pierre Sauvage découlent avant tout de conceptions topologiques, plus proches de la géométrie. Une molécule qualifiée de topologiquement triviale est une molécule dont sa représentation dans le plan ne comporte aucune intersection entre liaisons. La molécule de $C_{60}$, comportant 60 atomes de carbones, totalement tridimensionnelle ayant la forme d'un ballon de football, peut être représentée (par un diagramme de Schlegel) totalement plane et ne présentant aucune intersection. En revanche, les molécules entrelacées, appelée caténanes ou rotaxanes sont topologiquement non triviales et les bases des machines moléculaires.

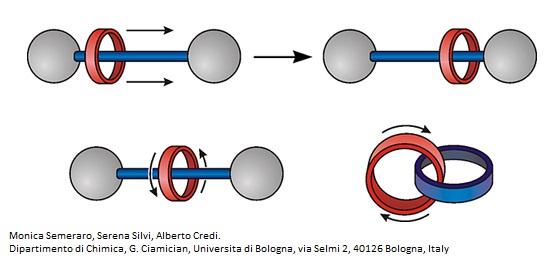Machines moléculaires primitives : caténanes et rotaxanes

Machines moléculaires que l'on retrouve en biologie et dont le vivant en est équipé, sous forme de protéines capables de transporter la matières d'un endroit à un autre. Mais la topologie est aussi présente d'une autre manière en biologie, et on la retrouve notamment dans la forme que prend l'ADN et par le nombre de croisements des nœuds.