Contexte
Dans cet univers immense qui est le nôtre, il existe un
certain nombre de corps stellaires nous offrant la possibilité de le
cartographier et ainsi de mieux le comprendre. C’est pourquoi nous
allons nous intéresser à des étoiles particulières, les Céphéides, qui
vont nous permettre d’étalonner les échelles de distance dans
l’Univers grâce à leurs propriétés particulières. Revenons un peu en
arrière... En 1784, John Goodricke, astronome, fait la découverte de
deux étoiles variables : δ Cep et β Lyrae. Ces étoiles
variables, anciennement appelées étoiles « changeantes », possèdent la
propriété suivante : leur éclat varie périodiquement au cours du
temps. Les Céphéides, du nom de la constellation où elles furent
découvertes, sont aussi appelées étoiles pulsantes puisqu’en plus de
leur variation de luminosité, on note chez elles une variation de
rayon, périodique au cours du temps. Ces étoiles présentent
effectivement une alternance périodique d'expansion et de contraction
de leurs couches superficielles, incluant leur atmosphère. Nous
observons ainsi une variation de diamètre au cours du temps, de
l’ordre de 10% pour l’ensemble des Céphéides. La période de pulsation
de ces étoiles est de quelques jours à plusieurs semaines. Les
paramètres de l Car, Céphéide qui fait l’objet de notre étude, sont
les suivants :

Tableau 1 : Paramètres de la
Céphéide l Car [1] [6]
En étudiant les Céphéides du Grand Nuage de Magellan
(ou LMC - Large Magellanic Cloud), une astronome américaine,
Henrietta Swan Leavitt [2] découvre
en 1912 que la période de pulsation est corrélée à la magnitude
apparente moyenne. Une fois étalonnée, cette relation deviendra la
relation Période-Luminosité des Céphéides.
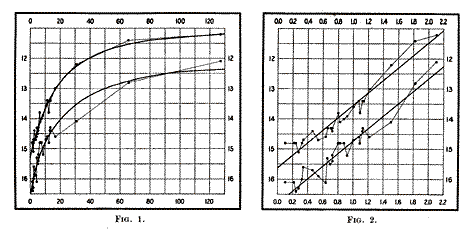
FIGURE 1 : Diagramme de la relation
entre la période et la magnitude apparente découverte par H. Leavitt
pour les Céphéides du LMC [3]. A
gauche, magnitude apparente (maximum et minimum) en fonction de la
période. A droite : magnitude apparente (maximum et minimum) en
fonction du logarithme de la période.
L'étalonnage de la relation Période-Luminosité est un
point clef pour utiliser les Céphéides comme indicateurs de distance.
Afin de calibrer celle-ci (c'est-à-dire déterminer la pente et le
point-zéro de la relation de la Figure 1), il
faut connaître la distance des Céphéides proches.
En effet, si on connait la distance des Céphéides proches
(d), on en déduit leur magnitude absolue (Mv) grâce au module de la
distance :
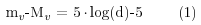
avec mv la magnitude apparente. On mesure ensuite la période de
l'étoile, et par la relation :
avec P la période de l'étoile et <Mv> sa magnitude
absolue moyenne,on trouve la pente a et le point zéro b.
Ainsi, une fois que l'on connait la pente et le point zéro
de la relation Période-Luminosité, que l'on mesure la période et la
magnitude apparente moyenne d'une Céphéide de distance quelconque, on
retrouve sa magnitude absolue moyenne par la relation (2) et on en déduit
sa distance par la relation (1).
Ainsi, les deux méthodes principales pour calibrer cette relation sont la
parallaxe trigonomètrique et la parallaxe de la pulsation [6],
qui s'appliquent aux Céphéides de la Voie Lactée.
La parallaxe trigonométrique :
Cette mesure consiste à observer deux fois, à six mois
d'intervalle, l'objet dont on veut connaître la distance, ceci afin
d'utiliser la position de la Terre à deux instants diamétralement opposés
et donc maximiser la base permettant de mesure la parallaxe (π en seconde
d'arc). C'est une méthode adaptée aux étoiles les plus proches dont la
distance (en parsecs) est proportionnelle pour de très petits angles, à
l'inverse de la parallaxe :
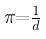
A noter : 1 pc est la distance d'un objet présentant une
parallaxe d'une seconde d'arc et par ailleurs, 1 pc = 3.26 a.l. De nos
jours, on utilise la parallaxe trigonométrique depuis l'espace grâce au
satellite d'observation Hipparcos et grâce à l'actuel satellite Gaia.
Cependant, la méthode de la parallaxe trigonométrique ne
permet que de mesurer (avec une bonne précision) des distances allant
jusqu’à 3 kpc (moins de 10 000 années-lumière) alors que la méthode de
la parallaxe de la pulsation, que j’expliquerai plus tard car nous nous
servirons de cette méthode, a permis de mesurer des distances allant
jusqu'au LMC, situé à 50 kpc environ (~ 163 000 années-lumière).
Les Céphéides ont permis de comprendre l’Univers :
L’étude des Céphéides a permis à Harlow Shapley
(1885-1972), astrophysicien américain de montrer en 1918 [4]
que le Soleil n’est pas situé au centre de notre galaxie, la Voie
Lactée. Pour cela, il a observé des Céphéides de type 2 (contenant moins
de métaux) dans des amas globulaires. Un autre exemple fondamental qui
prouve l’importance des Céphéides concerne l’astronome américain Edwin
Hubble (1889-1953). À l’aide de clichés pris avec un téléscope géant,
Hubble [5] a réussi à calculer la
distance qui nous sépare de la galaxie d’Andromède, grâce à la relation
Période-Luminosité de ces étoiles variables. Il a ainsi montré en 1925
que la galaxie d’Andromède était hors de notre système stellaire, à
environ 2 millions d’années-lumière. Ces observations ont prouvé que
notre galaxie n’était qu’une goutte d’eau parmi les milliards d’autres
galaxies formant notre univers. Après calibration, la relation
Période-Luminosité permet ainsi de mesurer des distances allant jusqu'à
40 Mpc (~ 100 millions d'années-lumière) (cf. Figure 2).
Après son succès avec la galaxie d’Andromède, Hubble a continué ses
recherches. Il note en 1929 une relation de proportionnalité entre la
distance des galaxies et leur vitesse d’éloignement, une des théories
clefs de l’expansion de l’univers. Cette relation est aujourd’hui connue
sous le nom de loi de Hubble :
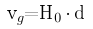
avec vg la vitesse d'éloignement de la galaxie (en km/s),
d sa distance (en Mpc) et Ho la constante de Hubble (en km/s/Mpc).
FIGURE 2 : Les distances dans l’Univers
(Crédits : Richard Powell : http
://atunivers.free.fr). (a) La Voie Lactée entourée par plusieurs
galaxies naines dont le Grand Nuage de Magellan. (b) Le Groupe Local. (c)
Le Superamas de la Vierge. Pour ces distances, la relation
Période-Luminosité des Céphéides est incontournable. (d) Les Superamas
Voisins. À ces grandes distances, on utilise des objets particuliers tels
que les supergéantes, les amas globulaires et les supernovae. A plus
grande distance, on utilise la loi de Hubble.
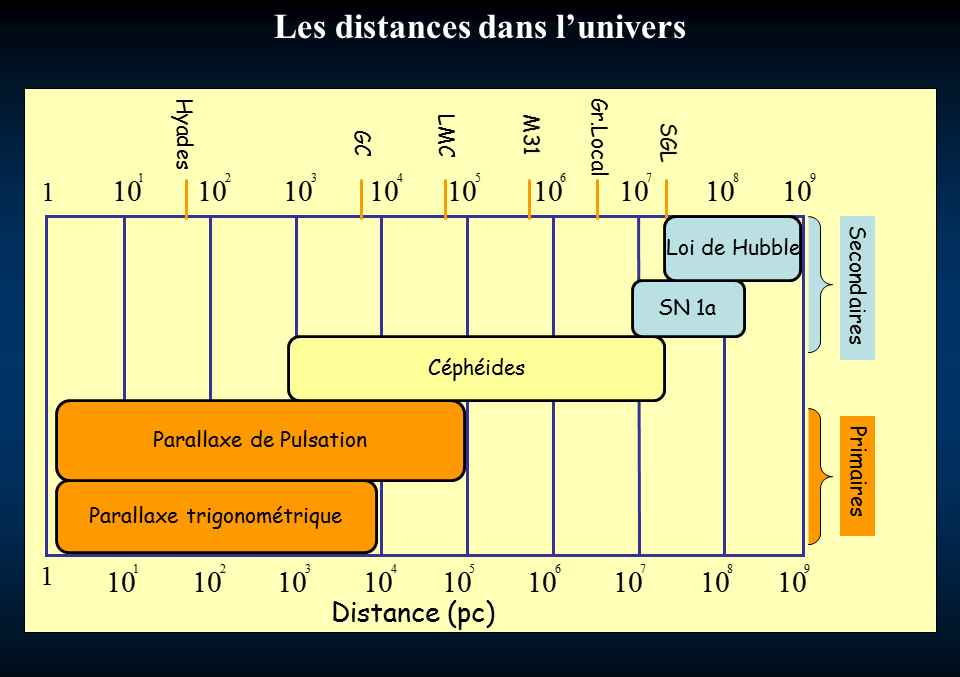
FIGURE 3 : Les méthodes utilisées pour déterminer les
distances dans l'Univers. (Source : Thèse de Nicolas Nardetto [11])