Chaines élastique : Isolant topologique mécanique

Pour cette étude nous nous sommes inspirés des publications de Prof. V. Vitelli qui sont disponibles dans les références.

Modèle 1D

Comme schématisé sur la figure ci-dessous, le modèle consiste en un arrangement périodique (périodicité $a$) de rotors rigides sans masses de longueur $r$ (traits noirs), en rotation autour de points de pivot (croix noires) d’un angle à l’équilibre de $\theta$ pour les sites pairs $n$ et de $\pi - \theta$ pour les sites impairs $n+1$. Les cercles bleus représentent des masses ponctuelles $M$, et le trait pointillé rouge un ressort de raideur $k$ et de longueur à l’équilibre $l$.

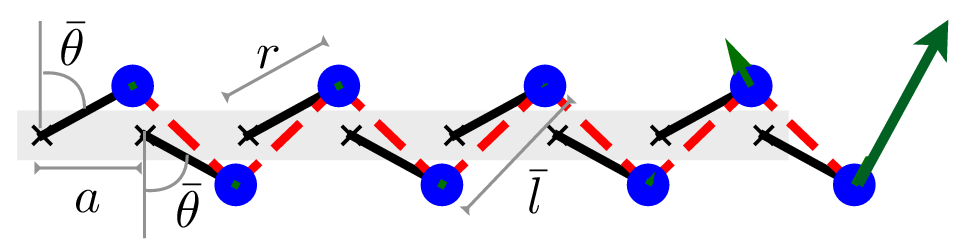
topo1.png

On va linéariser le problème pour des faibles oscillations $\delta\theta_n$ et $\delta\theta_{n+1}$ autour des positions d'équilibre.

Cas de deux masses couplées par un ressort

  • On commence avec un cas simple, un système constitué de 2 sites comme le montre la figure ci-dessous :

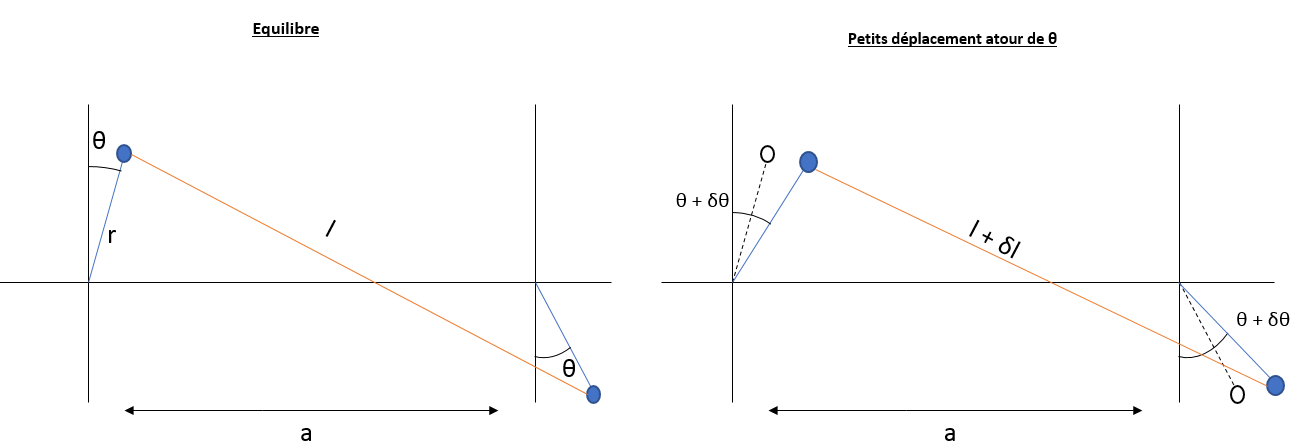
chaine.png

Résolution analytique

On traite donc le problème en calculant l'énergie mécanique du système :

  • Pour commencer on aura besoin de connaitre $l$ et $\delta l$ pour calculer l'énergie potentielle:

    $l = \sqrt{a^2 + 4 r^2 \cos^2(\theta)}$

    $\delta l = \frac{r\cos(\theta)}{l} [2r\sin(\theta) + a] \delta \theta_1 + \frac{r\cos(\theta)}{l} [2r\sin(\theta) - a] \delta \theta_2$

Pour simplifier l'équation on écrit :

$\delta l = c_1 \delta \theta_1 + c_2 \delta \theta_2$

On peut à présent calculer les énergies du système en question :

L'énergie potentielle : $E_p = \frac{1}{2}k(\delta l )^2$

L'énergie cinétique : $E_c = \frac{1}{2}M r^2 \delta\dot{\theta_1}^2 + \frac{1}{2}M r^2 \delta\dot{\theta_2}^2$

L'énergie mécanique : $E_m = E_c + E_p$

L'énergie mécanique se conserve, on applique donc $\frac{dE_m}{dt} = 0$ pour retrouver les équations du mouvement.

$\frac{dE_m}{dt} = k \delta l \dot{\delta l} + M r^2 \delta\dot{\theta_1} \delta\ddot{\theta_1} + M r^2 \delta\dot{\theta_2}\delta\ddot{\theta_2}$

$0 = k(c_1 \delta\theta_1 + c_2 \delta\theta_2)(c_1 \delta\dot{\theta_1} + c_2 \delta\dot{\theta_2}) + M r^2(\delta\dot{\theta_1}\delta\ddot{\theta_1} + \delta\dot{\theta_2}\delta\ddot{\theta_2})$

\begin{equation} \begin{pmatrix} \delta\dot{\theta_1} (M r^2 \delta\ddot{\theta_1} + k c_1^2 \delta\theta_1 + k c_1 c_2 \delta\theta_2) \\ \delta\dot{\theta_2} (M r^2 \delta\ddot{\theta_2} + k c_2^2 \delta\theta_2 + k c_1 c_2 \delta\theta_1) \end{pmatrix} =0 \end{equation}

Ainsi on a donc :

\begin{equation} \begin{pmatrix} \delta\ddot{\theta_1} \\ \delta\ddot{\theta_2} \end{pmatrix} =\frac{k}{M r^2} \begin{pmatrix} c_1^2 & c_1 c_2 \\ c_1 c_2 & c_2^2 \end{pmatrix} \begin{pmatrix} \delta\theta_1 \\ \delta\theta_2 \end{pmatrix} \end{equation}

En posant $\delta\theta_i = \delta\theta_{i,0}e^{\omega t}$ on retrouve une équation aux valeurs propres :

\begin{equation} A \delta\theta_0 = \omega^2 \delta\theta_0 \end{equation}

Où $A$ représente :

\begin{equation} \begin{pmatrix} c_1^2 & c_1 c_2 \\ c_1 c_2 & c_2^2 \end{pmatrix} \end{equation}

Cas de trois masses couplées par deux ressorts

  • Ayant trouvé comment résoudre les équations du système précédent on se propose de suivre le même raisonnement pour un cas un peu plus complexe d'une chaine composée de 3 masses et 2 ressorts comme on peut le voir ci-dessous. On pourra par la suite, grâce à cette résolution, généraliser le système à $N$ masses et $N-1$ ressorts.

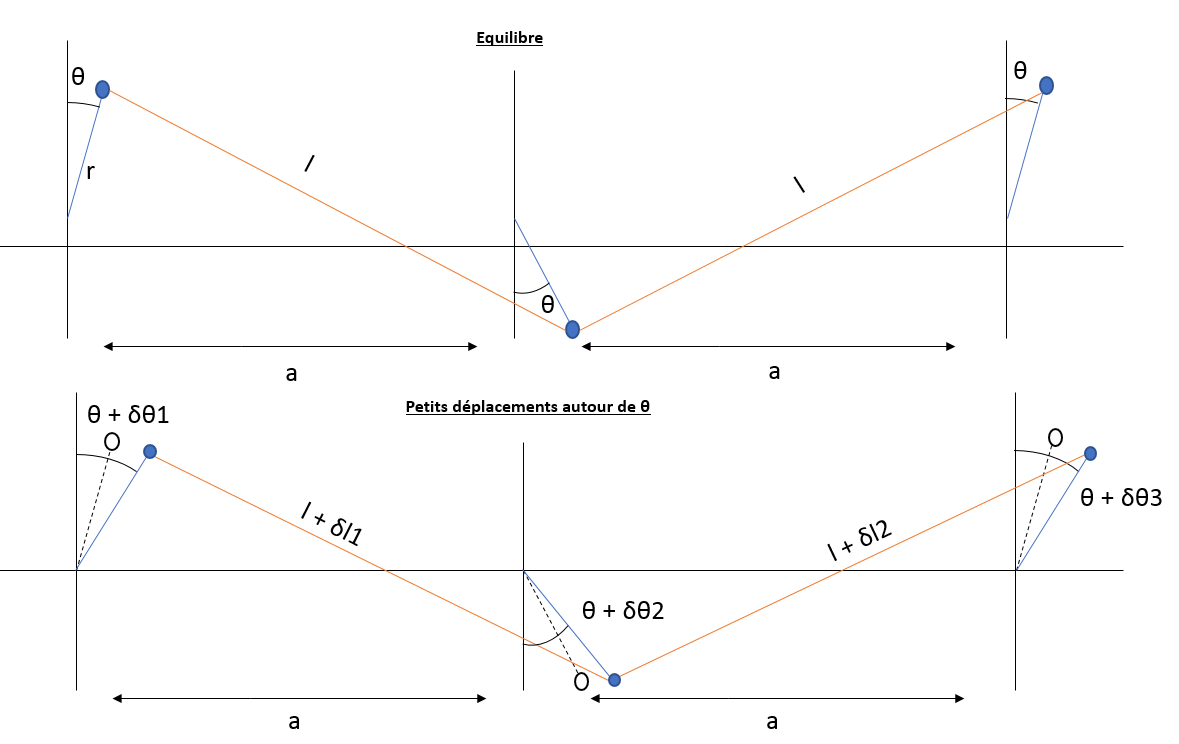
chaine2.png

Résolution analytique

On suit les même étape que dans la partie 1.1 en calculant l'énergie mécanique du système :

  • Il faut cependant prendre en compte que les $\delta l_1$ et $\delta l_2$ sont différents, on a en effet :

\begin{equation} \delta l_1 = \frac{r\cos(\theta)}{l} [2r\sin(\theta) + a] \delta \theta_1 + \frac{r\cos(\theta)}{l} [2r\sin(\theta) - a] \delta \theta_2 \\ \delta l_2 = \frac{r\cos(\theta)}{l} [2r\sin(\theta) - a] \delta \theta_2 + \frac{r\cos(\theta)}{l} [2r\sin(\theta) + a] \delta \theta_3 \end{equation}

  • On peut simplifer les deux équations par :

\begin{equation} \delta l_1 = c_1 \delta\theta_1 + c_2 \delta\theta_2 \\ \delta l_2 = c_2 \delta\theta_2 + c_3 \delta\theta_3 \end{equation}

  • On remarquera que :

\begin{equation} \sum_{n=0}^{\infty} c_{2n+1} = \frac{r\cos(\theta)}{l} [2r\sin(\theta) + a] = c_1\\ \sum_{n=0}^{\infty} c_{2n} = \frac{r\cos(\theta)}{l} [2r\sin(\theta) - a] = c_2 \end{equation}

On procède donc au calcul de l'énergie mécanique du système :

\begin{equation} E_m = \frac{1}{2}k(\delta l_1 )^2 + \frac{1}{2}k(\delta l_2 )^2 + \frac{1}{2}M r^2 \delta\dot{\theta_1}^2 + \frac{1}{2}M r^2 \delta\dot{\theta_2}^2 +\frac{1}{2}M r^2 \delta\dot{\theta_3}^2 \end{equation}

Comme précédemment l'énergie mécanique ce conserve $\frac{dE_m}{dt} = 0$, on en déduit la matrice suivante :

\begin{equation} \begin{pmatrix} \delta\ddot{\theta_1} \\ \delta\ddot{\theta_2} \\ \delta\ddot{\theta_3} \end{pmatrix} =\frac{k}{M r^2} \begin{pmatrix} c_1^2 & c_1 c_2 & 0\\ c_1 c_2 & 2c_2^2 & c_2 c_3 \\ 0 & c_2 c_3 & c_3^2 \end{pmatrix} \begin{pmatrix} \delta\theta_1 \\ \delta\theta_2 \\ \delta\theta_3 \end{pmatrix} \end{equation}

On peut donc facilement déduire la matrice d'un système N masses couplées.

Résolution Numérique

Suite à la résolution analytique du système mécanique on s'intéresse au spectre du système, pour cela on fait appel au programme affiché ci-dessous : On se place dans un cas fini pour N sites.

In [4]:
import numpy as np
import numpy.linalg as alg
import matplotlib
import scipy.integrate as integrate
import scipy.special as special
import matplotlib.pyplot as plt
from numpy import cos, sin, pi, exp, arctan
from scipy import misc
from scipy.integrate import quad

# Pour Systeme fini :
def set_C(theta=0., a=1., r=1., k=1., M=1., parity='odd'):
    l = np.sqrt(a**2 + 4*r**2*cos(theta)**2)
    if parity is 'odd':
        return np.sqrt(k/M)*(1/r)*(r*cos(theta)/l)*(2*r*sin(theta)+a)
    elif parity is 'even':
        return np.sqrt(k/M)*(1/r)*(r*cos(theta)/l)*(2*r*sin(theta)-a)

def set_chain(C1, C2, N):
    C = np.zeros(N)
    for i in range(N):
        if i%2==0:
            C[i] = C1
        else:
            C[i] = C2
    return C

def define_matrix(C, boundary='free'):
    A_diag = np.zeros(len(C))
    for i in range(0, len(C)-2):
        A_diag[i+1] = 2*C[i+1]**2
    A_diag_p = [C[i]*C[i+1] for i in range(len(C)-1)]
    A_diag_m = [C[i]*C[i+1] for i in range(len(C)-1)]
    A = np.diag(A_diag) + np.diag(A_diag_m, -1) + np.diag(A_diag_p, 1)
    if boundary is 'free':
        for i in [0, -1]:
            A[i,i] = C[i]**2
    elif boundary is 'periodic':
        A[0,0] = 2*C[0]
        A[-1,-1] = 2*C[1]**2
        A[-1,0] = C[0]*C[1]
        A[0,-1] = C[0]*C[1]

    return A

def diag_matrix(A):
    u, v = alg.eig(A)
    # Sort eigenvalues/vectors
    idx = np.argsort(u)
    u_sorted = [u[i] for i in idx]
    v_sorted = np.zeros(v.shape)
    for i in range(N):
        for j in range(N):
            v_sorted[i,j]=v[i,idx[j]]
    return u_sorted, v_sorted

def plot_spectra_with_theta(theta, N, a=1., r=1., k=1., M=1., fignum=None, boundary='free'):
    plt.figure(fignum)
    plt.clf()
    for i in range(len(theta)):
        C1 = set_C(theta=theta[i], a=a, r=r, k=k, M=M, parity='odd')
        C2 = set_C(theta=theta[i], a=a, r=r, k=k, M=M, parity='even')
        C = set_chain(C1, C2, N)
        A = define_matrix(C, boundary=boundary)
        u, v = diag_matrix(A)
        plt.plot([theta[i]]*N, u, 'bo')
    plt.xlabel('$Theta$')
    plt.ylabel('Spectra')
    plt.show()

def plot_wavefunction(v, index, intensity=False, fignum=None):
    plt.figure(fignum)
    plt.clf()
    for i in index:
        i = int(i)
        x = np.linspace(0, len(v), len(v))
        y = [i]*len(v)
        if intensity:
            v_int = np.abs(v[:,i])**2
            plt.scatter(x, y, c=v_int, cmap='Reds')
        else:
            plt.scatter(x, y, c=v[:,i], cmap='bwr', vmin=-1, vmax=1.)
    plt.colorbar()
    plt.xlabel('$N° du site$')
    plt.ylabel('Valeurs propres')
    plt.title('Amplitude')
    plt.show()
In [6]:
N = 50
r = 1.2
a = 1.
k = 1.
M = 1.

# Plot with theta
theta_list = np.linspace(-0.1, 0.1, 51)
plot_spectra_with_theta(theta_list, N, a=a, r=r, k=k, M=M, fignum=1)

# Plot for typical theta values
theta = [-0.1, 0., 0.1]
plt.figure(2)
plt.clf()
x = np.linspace(0, N, N)
for t in theta:
    C1 = set_C(theta=t, a=a, r=r, k=k, M=M, parity='odd')
    C2 = set_C(theta=t, a=a, r=r, k=k, M=M, parity='even')
    # Mode propre et sites
    C = set_chain(C1, C2, N)
    A = define_matrix(C)
    u, v = diag_matrix(A)
    plt.scatter(x, [t]*N, c=v[:,25], cmap='bwr', vmin=-1, vmax=1.)
plt.xlabel('$N° du site$')
plt.ylabel('Theta');

Le premier graphique nous montre la relation de dispersion de la matrice du système étudié plus haut avec $N=50$ sites (i.e. masses). On remarque que le spectre est gappé lorsque $\theta \neq 0 $, de plus un état propre se situe à l'intérieurd du gap, il représente un mode de bord du système. Ce mode de bord peut se représenter par de petites oscillations de la masse se trouvant à l'extrémité de la chaine sans exciter les masses voisines.

Le second graphique nous montre l'amplitude de déplacement du site en fonction de $\theta$, il cible les états propres à l'intérieur du gap pour $\theta = \{ -0.1, 0, 0.1 \} $. On voit clairement que l'exciation du site est localisée sur une extrémité :

  • Lorsque $\theta < 0 $ le mode est localisé à droite

  • Lorsque $\theta > 0 $ le mode est localisé à gauche

  • Lorsque $\theta = 0 $ c'est à dire à la position d'équilibre, le système n'est plus gappé et le mode est délocalisé.

In [1]:
from IPython.display import HTML
HTML('''<script>
code_show=true; 
function code_toggle() {
 if (code_show){
 $('div.input').hide();
 } else {
 $('div.input').show();
 }
 code_show = !code_show
} 
$( document ).ready(code_toggle);
</script>
Le code python de ce notebook est caché pour une meilleure lecture de la page.
Pour afficher/désafficher le code, cliquez <a href="javascript:code_toggle()">ici</a>.''')
Out[1]:
Le code python de ce notebook est caché pour une meilleure lecture de la page. Pour afficher/désafficher le code, cliquez ici.