Winding number¶

La matrice de rigidité joue un rôle essentiel dans la détermination du "winding number" noté $n$ qui décrit un invariant topologique. On s'intéresse donc au déterminant de la matrice de compatibilité $C$.

La matrice $C(q) \equiv |C(q)| e^{i \Phi} $ se caractérise dans la zone de Brillouin $(-\pi/a <q < \pi/a)$ par un chemin de le plan complexe. Comme il dépend de $e^{ika}$ le chemin se fermera en retournant à son point de départ lorsque $q$ évolue dans la zone de Brillouin. C'est courbes sont caractérisées par le "winding number", c'est à dire le nombre d'enroulement :

\begin{equation} n= \frac{1}{2 \pi} \int_{\frac{-\pi}{a}}^{\frac{\pi}{a}} dq \frac{d \Phi(q)}{dq} \\ Où \\ \Phi (q) = arg(det|C(q)|) \end{equation}

On retrouve donc soit $n=0$ soit $n=1$. Dans le premier cas, les chemin dans le plan complexe ne s'enroule pas autour de l'origine, dans le second cas, le chemin s'enroule bien autour de l'origine.

Le winding number est un invariant topologique qui vaut $ 1 $ pour tout $ -\pi<\theta<0$ et $ 0 $ pour tout $ 0< \theta < \pi$. Le seul moyen de changer la valeur de $n$ est en passant par un angle critique $\theta = 0$ ou $\theta = \pi$. Lorsque $n=0$, le zero mode se localise sur la droite, et quand $n=1$ le zero mode se localise sur la gauche.

Afin de vérifier si la matrice trouvée est bonne on étudie le winding number dans les deux cas de $\theta$.

On considère donc $ \Phi (q) = \arctan ( \frac{\Im(C(q))}{\Re(C(q))}) $

Où

\begin{align} \Im(C(q)) = -c_2 \sin (qa) \\ \Re (C(q)) = c_1 - c_2 \cos (qa) \end{align}

Si on trace $ \Im(C(q)) $ en fonction de $ \Re (C(q)) $ dans la zone de Brillouin on retrouve :

import numpy as np
import numpy.linalg as alg
import matplotlib
import scipy.integrate as integrate
import scipy.special as special
import matplotlib.pyplot as plt
from numpy import cos, sin, pi, exp, arctan
from scipy import misc
from scipy.integrate import quad
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)

theta = -0.1
r = 1.
a = 0.8
l = np.sqrt(a**2 + 4*r**2*cos(theta)**2)
C1 = (r*cos(theta)/l)*(2*r*sin(theta)+a)
C2 = (r*cos(theta)/l)*(2*r*sin(theta)-a)

k = np.linspace(-pi/a, pi/a, 100)
Im_q = -C2*sin(k*a)
Re_q = C1 - C2*cos(k*a)

plt.figure(2)
plt.clf()
plt.plot(Re_q, Im_q, 'b')
plt.plot([0,0],[-1,1], 'k--')
plt.xlabel('$Re(q)$')
plt.ylabel('Im(q)')
plt.title('$Theta$ = {}'.format(theta))
plt.axis('equal')
plt.xlim([-0.5,1])
plt.ylim([-0.5,0.5])
plt.show()

theta = 0.1
r = 1.
a = 0.8
l = np.sqrt(a**2 + 4*r**2*cos(theta)**2)
C1 = (r*cos(theta)/l)*(2*r*sin(theta)+a)
C2 = (r*cos(theta)/l)*(2*r*sin(theta)-a)
Im_q = -C2*sin(k*a)
Re_q = C1 - C2*cos(k*a)


plt.figure(3)
plt.clf()
plt.plot(Re_q, Im_q, 'b')
plt.plot([0,0],[-1,1], 'k--')
plt.xlabel('$Re(q)$')
plt.ylabel('Im(q)')
plt.title('$Theta$ = {}'.format(theta))
plt.axis('equal')
plt.xlim([-0.5,1])
plt.ylim([-0.5,0.5])

plt.show()

On retrouve donc bien un enroulement autour de l'origine pour un $\theta < 0 $, ce qui nous donnera un $n=1$ et dans le second graph $ \theta > 0 $, il n'y a pas d'enroulement autour de l'origine, $n=0$.

Le winding number a tout de même été calculé numériquement afin de vérifier notre relation analytique :

import numpy as np
import numpy.linalg as alg
import matplotlib
import scipy.integrate as integrate
import scipy.special as special
import matplotlib.pyplot as plt
from numpy import cos, sin, pi, exp, arctan
from scipy import misc
from scipy.integrate import quad


def dphi(k):
    dPhi = ((-C1*C2*a*cos(k*a) + C2**2 * a)/(C1-C2*cos(k*a))**2)/(1+((-C2*sin(k*a))/(C1-C2*cos(k*a)))**2)
    return dPhi

if __name__=='__main__':
    N = 4

    # Plot for single theta value
    theta = 0.1
    r = 1.
    a = 0.8
    l = np.sqrt(a**2 + 4*r**2*cos(theta)**2)
    C1 = (r*cos(theta)/l)*(2*r*sin(theta)+a)
    C2 = (r*cos(theta)/l)*(2*r*sin(theta)-a)


    # Plot for winding number
    k = np.linspace(-pi/a, pi/a, 100)
    Im_q = -C2*sin(k*a)
    Re_q = C1 - C2*cos(k*a)

    # Winding Number 
    dPhi = ((-C1*C2*a*cos(k*a) + C2**2 * a)/(C1-C2*cos(k*a))**2)/(1+((-C2*sin(k*a))/(C1-C2*cos(k*a)))**2)
    Phi = arctan(Im_q/Re_q)
    plt.figure(3)
    plt.subplot(121)
    plt.clf()
    plt.plot(k, Phi, 'b')
    plt.plot(k, dPhi, 'r')
    #plt.show()

    n = integrate.quad(dphi, -pi/a, pi/a)
    n = n[0]
    print('Theta =', theta)
    print('Winding number =', n*(1/(2*pi)))

    # Plot for single theta value
    theta = -0.1
    r = 1.
    a = 0.8
    l = np.sqrt(a**2 + 4*r**2*cos(theta)**2)
    C1 = (r*cos(theta)/l)*(2*r*sin(theta)+a)
    C2 = (r*cos(theta)/l)*(2*r*sin(theta)-a)


    # Plot for winding number
    k = np.linspace(-pi/a, pi/a, 100)

    # Winding Number 
    dPhi = ((-C1*C2*a*cos(k*a) + C2**2 * a)/(C1-C2*cos(k*a))**2)/(1+((-C2*sin(k*a))/(C1-C2*cos(k*a)))**2)
    Phi = arctan(Im_q/Re_q)
    #plt.figure(5)
    plt.subplot(122)
    plt.clf()
    plt.plot(k, Phi, 'b')
    plt.plot(k, dPhi, 'r')
    #plt.show()

    n = integrate.quad(dphi, -pi/a, pi/a)
    n = n[0]
    print('Theta =', theta)
    print('Winding number =', n*(1/(2*pi)))

Theta = 0.1
Winding number = -2.1822139064485795e-15
Theta = -0.1
Winding number = 1.0000000000000047

Polarisation topologique¶

Précédemmet on a vu que le winding number indique où se localise le zero mode. Pour étudier ce cas plus en détail on doit parler de polarisation topologique. Cette polarisation va dépendre de l'orientation des rotors, donc de l'angle $\theta$ au bord du système. Pour interpréter les deux valeurs obtenues du winding number on considère une chaine semi-infinie et on regarde ce qu'il se passe au bord.

Polarisation gauche¶

Lorsque le winding number $n=1$ on se retrouvre donc avec un angle négatif $(-\pi < \theta < 0)$, donc les rotors pointe vers la gauche, on peut voir que l'état de bord se localise sur la gauche, le reste de la chaine ne bouge pas.

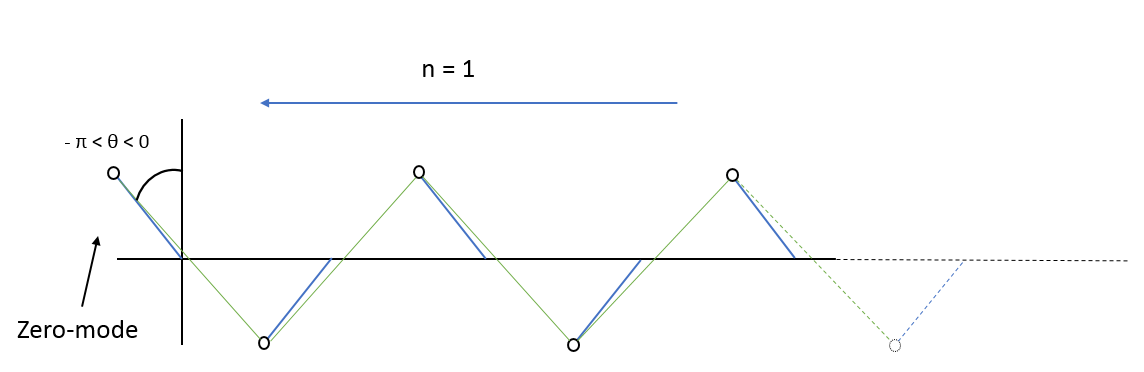
Polarisation droite¶

A présent on se place dans le deuxième cas où $n=0$, on considère encore une chaine semi-infini, ici $(0 < \theta < \pi ) $ le bord du système est a présent bloqué, si on considère une chaine finie, on pourra voir un état de bord (zero mode) de l'autre coté du système.

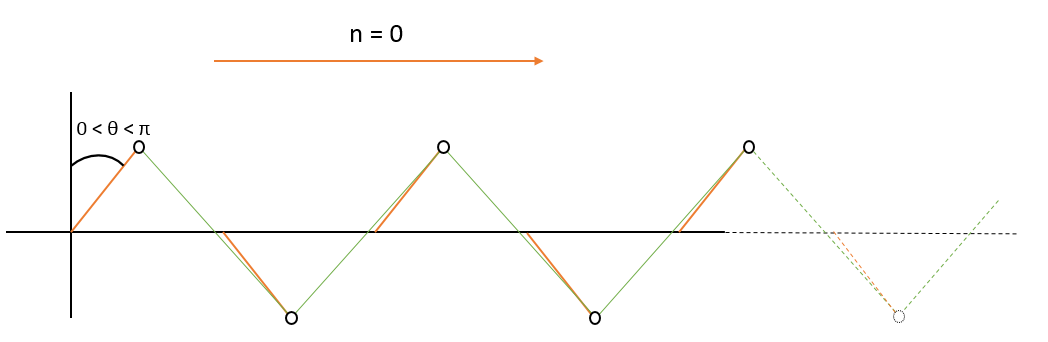
Interface entre deux polarisations¶

Kink/Domain wall¶

Dans le cas d'une interface $n=0$ et $n=1$ on va retrouver un domaine wall au milieu du système (cette fois ci la chaine est considérée comme infinie car on ne s'intéresse pas aux effets de bord)

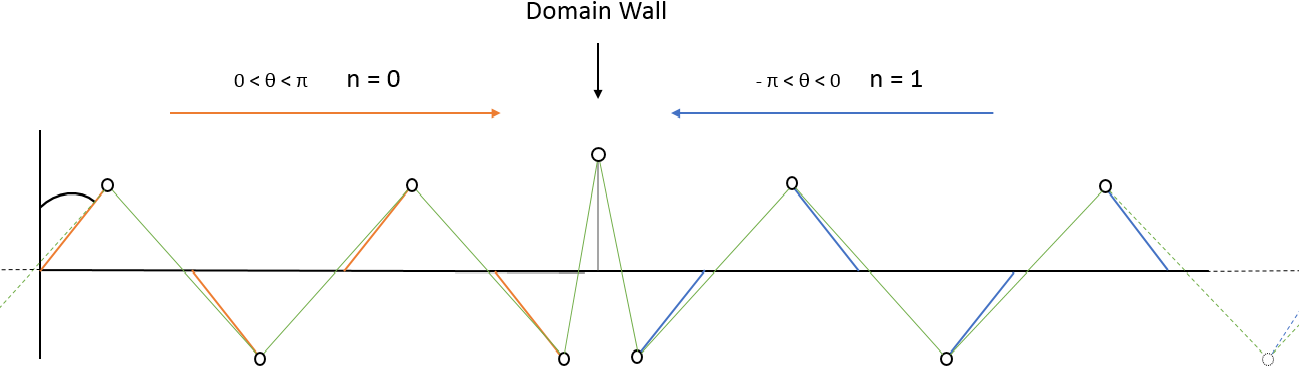
Ce "domain wall" ou kink représente un mode-zero, il est localisé dans le volume, le reste de la chaine reste immobile.

Anti-kink¶

Dans le cas d'une interface $n=1$ et $n=0$ on remarque un mode de selfstress a l'interface, si on se place dans un système fini cette configuration fera apparaitre deux modes de bords aux deux extrémités du système.

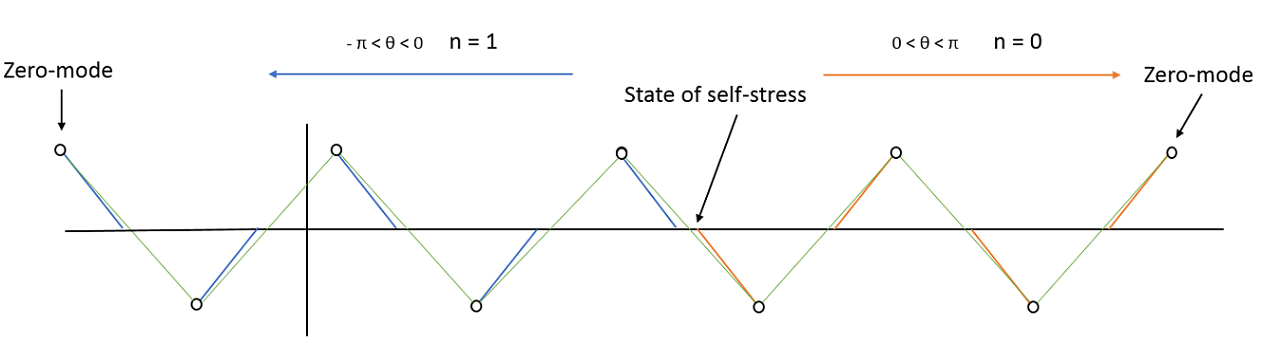
On peut expliquer ces modes de bords grâce à la relation vu précédemment $\nu = N_0 - N_s$ dans le schéma au dessus on à $\nu = 1$ car il y a un site de plus que de liens. De plus on sait qu'il y a un état de self-stress donc $N_s = 1 $ on en déduit donc facilement les nombres de "zero-mode" présent dans une telle configuration, soit $N_0 = 2 $.

Discussion¶

Cette analyse linéaire nous à permis de mettre en évidence l'invariant topologique d'un système mécanique simple à partir de sa configuration (sites et liens) et les différents modes associés à ce systèmes. Comme le système est à une dimension on ne peut pas noté le conducteur en surface d'un isolant topologique (la "conduction ne se fait que sur un point localisé sur le mode-zero). On à donc observé un système mécanique se comportant comme un isolant topologique.

Cependant, pour de grand déplacement du rotor (donc de $\theta$) autour de la position d'équilibre, le mode-zero se déplace tout au long de la chaine. Cela contredit ce que nous avons mis en évidence juste avant, néanmoins, ici l'analyse est non-linéaire dû aux grand déplacements, on pourra donc observer le transport d'un soliton dans le volume du système.

from IPython.display import HTML
HTML('''<script>
code_show=true; 
function code_toggle() {
 if (code_show){
 $('div.input').hide();
 } else {
 $('div.input').show();
 }
 code_show = !code_show
} 
$( document ).ready(code_toggle);
</script>
Le code python de ce notebook est caché pour une meilleure lecture de la page.
Pour afficher/désafficher le code, cliquez <a href="javascript:code_toggle()">ici</a>.''')