Mode-zero et états auto-contraints topologique dans un système 1D¶
On s'intéresse à présent à la relation entre le système mécanique étudié précédemment dans un cas générale puis périodique.
On va donc revoir le même système du 1$^{er}$ cas, cependant les notations seront différentes, ces notations faciliterons l'écriture de la matrice de rigidité et de la matrice de compatabilité.
Introduction¶
La rigidité joue un rôle essentiel dans l'ingénierie achitecturale, cependant les mathématiques de la rigidité de structure sont aussi une clef dans la compréhension des propriétés mécaniques de beaucoup de matériaux. Quand elle est modélisée en un réseau de masses et de ressorts, la rigidité et la souplesse de ces matériaux peuvent être compris en comparant les degrés de libertés des masses aux contraintes imposées par les ressorts.
Lorsque que trop peu de ressorts sont présent dans une structure, il y aura beaucoup de degrés de liberté qui rendront les matériaux en questions plus malléables, on pourra donc déformer la structure sans comprimer ou étendre les ressorts présent en son sein. Ces degrés de libertés sont appelés "zero-mode" ou mode-zero car il ne nécessite aucune énergie pour les exciter.
En revanche, lorsqu'il y a un surplus de ressorts dans la structure le matériaux n'aura plus aucun degrés de libertés, il ne subira pas de déformation mais certain de ses ressorts seront comprimés et/ou étendus. On appelle ces états "state of self-stress" ou encore états auto-contraints.
On peut distinguer plusieurs cas :
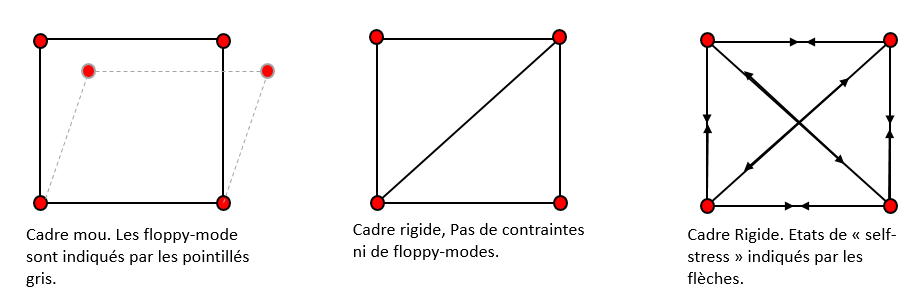
En 1864 Maxwell donne alors une relation liant 4 quantités très importantes dans une structure :
Le nombre de liens $N_B$
Le nombre de masses $N$ (connectés en $d$ dimension)
Le nombre de mode-zero $N_0$
Le nombre d'auto-contraintes ou "self stress" $N_S$
\begin{equation} \nu = dN - N_B = N_0 - N_S \end{equation}
Le cas qui nous intéresse est celui où $N_0 = N_S$, lorsqu'on se place dans un tel cas on dit que le système est "isostatique" ou "Maxwellian".
Théorie de la rigidité¶
On reprend a présent un système similaire à celui de la chaine élastique, cependant les notations changent, on va chercher un système de notations plus général pour le système mécanique étudié.
On considère donc un système avec des sites connectés entre eux par des liens. On assume que les liens et les sites ne seront ni détruit ni créé durant l'analyse, on peut donc noter les sites comme $s \in \{1,...,N\}$ et les liens comme $\beta \in \{1,...,N_B \}$. Chaque lien $\beta$ représente le lien entre un site $s_\beta$ et $s_\beta^\prime$ et peut être défini par pair $[ s_\beta, s_\beta^\prime ]$.
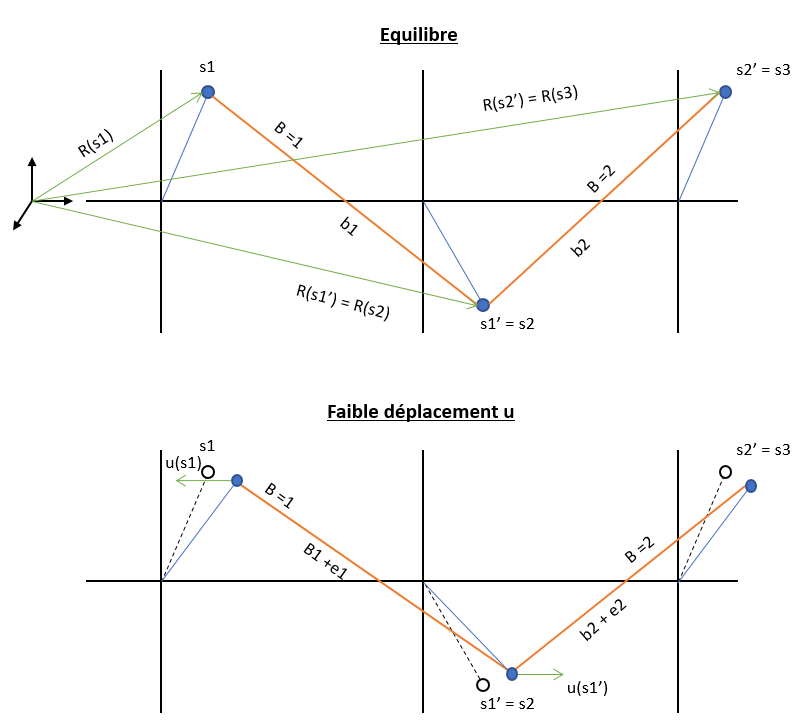
On rajoute une géométrie en assignant une position d'équilibre $R(s) \in \Re^d$ à tous les sites. Les liens reçoivent donc une valeur géométrique tel que $b_\beta = R(s_\beta^\prime) - R(s_\beta) $ que l'on nomme le vecteur de séparation.
Pour de petits déplacement autour de la position d'équilibre du système on peut étendre ou compresser les liens entre les sites. On note donc l'éllongation $e_\beta = \hat{b}_\beta ( u(s_\beta^\prime) - u( s_\beta) )$
Le schéma ci-dessous nous montre le système étudié pour la position d'équilibre et pour de faible déplacement $u$ autour de la position d'équilibre.
Calcul des forces¶
On note la tension des liens $t_\beta$ , la relation entre les forces agissant dans le système $f(s)$ et la tension des liens est linéaire, on a donc:
\begin{equation} \sum_{\beta:s\in\beta} -\varepsilon_{s,\beta} \hat{b}_\beta t_\beta \: \: où \: \: \varepsilon_{s,\beta} = \begin{Bmatrix} -1 \: si \: s = s_\beta\\ +1 \: si \: s = s_\beta^\prime \\ 0 \: \: sinon \end{Bmatrix} \end{equation}
- $-\varepsilon_{s,\beta} \hat{b}_\beta$ pointe toujours dans la direction opposée de $s$. On peut redéfinir l'élongation et la force tel que:
\begin{equation} e_\beta = \sum_{s,i} \varepsilon_{s,\beta} \hat{b}_{\beta,i} u_i(s) \; \: et \; \: f_i (s) = -\sum_\beta \varepsilon_{s,\beta} \hat{b}_{\beta,i} t_\beta \end{equation}
On peut donc appliquer ces expressions dans une matrice en prenant toutes les forces en $dN$ vecteurs de dimension et en prenant toutes les tensions en $N_B$ vecteurs de dimensions, soit: $U=(u(1),...,u(N))$; $F=(f(1),...,f(N))$; $E=(e_1,...,e_{N_B})$ et $T=(t_1,...,t_{N_B})$, on a donc :
\begin{equation} E=Q^T U \: \; et \; \: F = -QT \end{equation} Où les élément des la matrice de rigidité $Q$ de dimension $N_B * dN$ sont donnés par : \begin{equation} Q_{(s,i)\beta} = \varepsilon_{s,\beta} \hat{b}_{\beta,i} \end{equation}
Et $Q^T$ est la transposée de la matrice de rigidité $Q$, et est nommée matrice de compatibilité.
Application à la chaine élastique¶
Si on applique ces équations au système mécanique vu plus haut on trouve :
\begin{equation} E= \begin{pmatrix} e_1 \\ e_2 \end{pmatrix} \; \; \; U = \begin{pmatrix} u(1) \\ u(2) \\ u(3) \end{pmatrix} \; \; \; T= \begin{pmatrix} t_1 \\ t_2 \end{pmatrix} \; \; \; F= \begin{pmatrix} f(1)\\ f(2)\\ f(3) \end{pmatrix} \end{equation}
On peut donc former les matrices $Q$ et $Q^T$ :
\begin{equation} Q = \begin{pmatrix} \varepsilon_11 b_1 & \varepsilon_12 b_2 \\ \varepsilon_21 b_1 & \varepsilon_22 b_2 \\ \varepsilon_31 b_1 & \varepsilon_32 b_2 \end{pmatrix} = \begin{pmatrix} -b_1 & 0 \\ b_1 & -b_2 \\ 0 & b_2 \end{pmatrix} \; \; \; \; et \; \; \; \; Q^T = \begin{pmatrix} -b_1 & b_1 & 0 \\ 0 & -b_2 & b_2 \end{pmatrix} \end{equation}
Ces matrices sont très intéressantes pour la compréhension du comportement du système étudié, en effet $Q$ et $Q^T$ nous donnent des informations tel que les mode-zero et les auto-contraintes de la structure. Elle nous informe aussi de comportement dans le volume du système.
Lorsque $Q^T U =0$ on se retrouve dans le cas du cadre mou. On à bien un déplacement au niveau des liens, cependant, il n'y a aucune élongation.
Lorsque $QT=0$ on observe un cas similaire à celui du cadre rigide. La force nette exprimée sur les sites est nulle, en revanche il y a des élongations sur les liens.