Cas d'un système périodique¶
Introduction¶
Pour finaliser l'analyse linéaire d'une chaine élastique, on se place dans un cas périodique. Les systèmes périodiques sont composés de cellules contenant $n$ sites aux positions $s_1,...,s_n$. Ces cellules sont arrangées périodiquement au long d'un vecteur $a_i,...,a_d$.
Le système est composé de cellules notées $l = \{1,...,n \} $
Chaque cellules représente un suite de sites et liens.
Il y a 2 sites et 2 liens par cellules, notés respectivement : $s = \{1,2 \}$ et $ \beta = \{1,2 \}$.
On note $C = Q^\dagger$ la matrice de compatibilité.
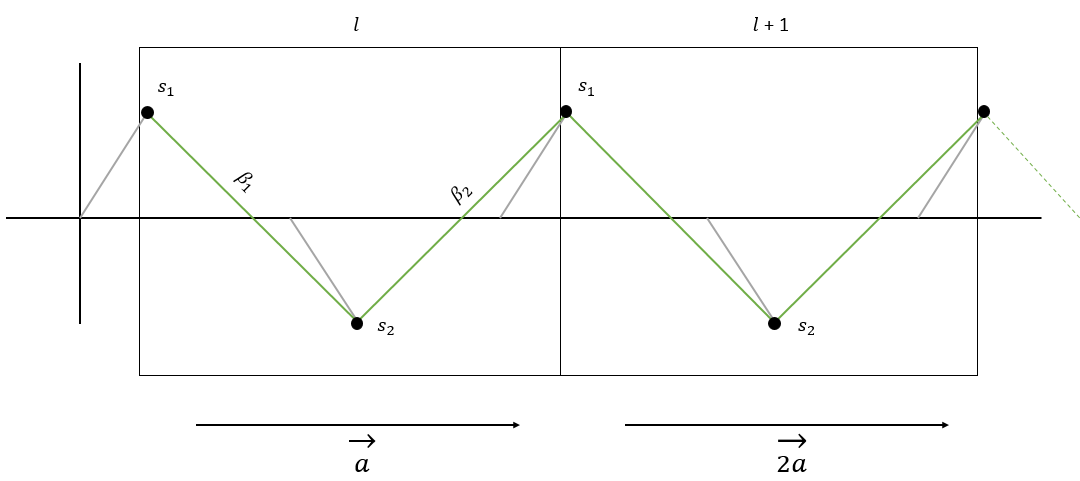
Le schèma ci-dessous représente le système en question :
Résolution analytique¶
On cherche donc à retrouver les matrices de rigidité et de compatibilité du système ($Q$ et $Q^T$). Pour cela on fait appel à la relation suivante :
\begin{equation} C_{\beta s} = c_1 \delta_{\beta, s} + c_2 \delta_{\beta , s \pm 1} \end{equation}
Où $\delta_{\beta, s} = 1$ si $\beta = s$ et $0$ sinon.
$C$ représente la matrice de compatibilité.
On note l'élongation des liens :
\begin{equation} \delta l_\beta = C_{\beta, s} \delta \theta_s \end{equation}
Prenons exemple sur notre système : on a donc $s = \{1,2 \}$ et $ \beta = \{1,2 \}$. On peut calculer $C_{\beta s}$ :
\begin{equation} C_{11} = c_1 \delta_{1,1} + c_2 \delta_{1,0} = c_1 \\ C_{12} = c_1 \delta_{1,2} + c_2 \delta_{1,1} = c_2 \\ C_{21} = c_1 \delta_{2,1} + c_2 \delta_{1,1} = c_2 \\ C_{22} = c_1 \delta_{2,2} + c_2 \delta_{2,1} = c_1 \end{equation}
Et on rappel que
\begin{equation} c_1 = \frac{r \cos(\theta)}{\sqrt(a^2 + 4 r^2 \cos^2(\theta))} [2 r \sin(\theta) + a ]\\ c_2 = \frac{r \cos(\theta)}{\sqrt(a^2 + 4 r^2 \cos^2(\theta))} [2 r \sin(\theta) - a ] \end{equation}
On peut donc déterminer $\delta l_\beta$ :
\begin{equation} \delta l_1 = C_{11} \delta \theta_1 + C_{12} \delta \theta_2 \\ \delta l_2 = C_{21} \delta \theta_1 + C_{22} \delta \theta_2 \end{equation}
En simplifiant on retrouve :
\begin{equation} \begin{pmatrix} \delta l_1 \\ \delta l_2 \end{pmatrix} = \begin{pmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{pmatrix} \begin{pmatrix} \delta \theta_1 \\ \delta \theta_2 \end{pmatrix} \end{equation}
On inclut à présent la notion de périodicité pour généraliser le calcul à $l$ cellules.
Le changement implique donc que : $\delta l_\beta = \delta l_{\beta, l } $
Exemple¶
\begin{equation} \begin{pmatrix} \delta l_1 \\ \delta l_2 \\ \delta l_3 \\ \delta l_4 \\ . \\ . \\ \end{pmatrix} \begin{pmatrix} \delta l_{1,0} \\ \delta l_{2,0} \\ \delta l_{1,1} \\ \delta l_{2,1} \\ . \\ . \\ \end{pmatrix} \end{equation}
- On peut représenter les $\delta l_{\beta , l}$ :
\begin{equation} \delta l_{1 , l} = C_{11} \delta \theta_{1,l} + C_{12} \delta \theta_{2,l} \\ \delta l_{2,l} = C_{21} \delta \theta_{2,l} + C_{22} \delta \theta_{1,l+1} \end{equation}
Si on rassemble tous les allongements $\delta l_{\beta,l}$ on peut former un vecteur $E(q) =( \delta l_1(q), \delta l_2(q))$, de même on peut rassembler tous les déplacements $\delta \theta_s$ pour former un vecteur $U(q) = ( \delta \theta_1 (q), \delta \theta_2 (q) )$.
En les rassemblant on retrouve les équations vues dans la partie "Théorie" $ E = Q^T U$ où $Q^T = C$.
Transformée de Fourier¶
Comme on se trouve dans un système périodique on peut appliquer la TF pour obtenir les variables précédentes en fonction du nombre d'onde $q$.
\begin{equation} \delta l_\beta (l) = \frac{1}{N_c} \sum_q e^{iqla} \delta l_\beta (q) \\ \delta \theta_s (l) = \frac{1}{N_c} \sum_q e^{iqla} \delta \theta_s (q) \end{equation}
On transfert ces equations dans $\delta l_\beta$
\begin{align} \delta l_1 (l) = c_1 \delta \theta_1 (l) + c_2 \delta \theta_2 (l) \\ \delta l_2 (l) = c_1 \delta \theta_2 (l) + c_2 \delta \theta_1 (l+1) \\ \end{align}
\begin{align} \delta l_1 (q) e^{iqla} = c_1 e^{iqla} \delta \theta_1 (q) + c_2 e^{iqla} \delta \theta_2 (q) \\ \delta l_2 (q) e^{iqla} = c_1 e^{iqla} \delta \theta_2 (q) + c_2 e^{iq(l+1)a} \delta \theta_1 (q) \\ \end{align}
\begin{align} \delta l_1 (q) = c_1 \delta \theta_1 (q) + c_2 \delta \theta_2 (q) \\ \delta l_2 (q) = c_2 e^{iqa} \delta \theta_1 (q) + c_1 \delta \theta_2 (q)\\ \end{align}
On peut en déduire les matrice de compatibilité et de rigidité dans l'espace de Fourier :
\begin{equation} C(q) = \begin{pmatrix} c_1 & c_2 \\ c_2 e^{iqa} & c_1 \end{pmatrix} \;\;\;\; et \;\;\; Q(q) = C^\dagger (q) = \begin{pmatrix} c_1 & c_2 e^{-iqa} \\ c_2 & c_1 \end{pmatrix} \end{equation}
On retrouve donc la matrice dynamique : \begin{equation} D = Q Q^T = \begin{pmatrix} c_1^2 + c_2^2 & c_1 c_2 (1 + e^{-iqa} ) \\ c_1 c_2 (1 + e^{iqa}) & c_1^2 + c_2^2 \end{pmatrix} \end{equation}
En diagonalisant la matrice $D$ on peut retrouver la relation de dispersion :
import numpy as np
import numpy.linalg as alg
import matplotlib.pyplot as plt
from numpy import cos, sin, pi, exp
def define_matrix1(q, theta=0., r=0.5, a=1.):
l = np.sqrt(a**2 + 4*r**2*cos(theta)**2)
C1 = (r*cos(theta)/l)*(2*r*sin(theta)+a)
C2 = (r*cos(theta)/l)*(2*r*sin(theta)-a)
D = np.array([[2*C1**2, C1*C2*(1 + exp(-1j*q*a))], [C1*C2*(1 + exp(1j*q*a)), 2*C2**2]])
return D
def diag_matrix1(D):
N = len(D)
u, v = alg.eig(D)
# Sort eigenvalues/vectors
idx = np.argsort(u)
u_sorted = [u[i] for i in idx]
v_sorted = np.zeros(v.shape)
for i in range(N):
for j in range(N):
v_sorted[i,j]=v[i,idx[j]]
return u_sorted, v_sorted
if __name__=='__main__':
theta = 0.
r = 1.2
a = 1.
q_list = np.linspace(-pi/a, pi/a, 100)
w = []
for q in q_list:
D = define_matrix1(q, theta, r, a)
u, v = diag_matrix1(D)
w.append(u)
plt.figure(1)
plt.subplot(121)
plt.plot(q_list, np.abs(w))
plt.xlabel('$q$')
plt.ylabel('Spectra')
plt.title('$Theta$ = {}'.format(theta))
theta = 0.1
q_list = np.linspace(-pi/a, pi/a, 100)
w = []
for q in q_list:
D = define_matrix1(q, theta, r, a)
u, v = diag_matrix1(D)
w.append(u)
plt.subplot(122)
plt.plot(q_list, np.abs(w))
plt.xlabel('$q$')
#plt.ylabel('Spectra')
plt.title('$Theta$ = {}'.format(theta))
plt.tight_layout()
On s'aperçoit donc de l'ouverture et la fermeture du gap en fonction de l'angle $\theta$ donné, à l'équilibre, c'est à dire $\theta = 0 $ on à pas de gap, cependant, dès que $\theta$ varie faiblement autour de cette position d'équilibre on note l'ouverture du gap.
Localisation du mode zero¶
On considère la relation vue plus haut $C \delta \theta = \delta l$ cependant on considère que $\delta l = 0$, il n'y a donc pas d'élongations des liens.
On peut en déduire que $det |C(q)| = 0 $ et donc:
\begin{equation} c_1^2 - c_2^2 e^{iqa} = 0 \\ e^{iqa} = \frac{c_1^2}{c_2^2} \\ q = -i \frac{2}{a} ln(\frac{c_1}{c_2}) \end{equation}
La solution de l'équation est un nombre imaginaire, cela montre que le mode va être localisé, le nombre d'onde décroit exponentiellement.
from IPython.display import HTML
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
Le code python de ce notebook est caché pour une meilleure lecture de la page.
Pour afficher/désafficher le code, cliquez <a href="javascript:code_toggle()">ici</a>.''')