1-Interférences simple:
Lorsque les deux ondes Ψ1 et Ψ2 issues de chaque bras se superposent sur l'écran d'observation,
on peut observer 2 situations possibles:
- Soit, les deux vecteurs d'onde sont parfaitement parallèles entre eux. On observera
une intensité, uniforme plus ou moins brillante sur l'écran, selon si les deux ondes
interfèrent de manière constructive ou destructive . On dit que l'interféromètre est réglé en teinte
plate.
- Soit, il apparaît un angle entre les deux vecteurs d'onde, comme illustré dans la figure 1.4.
Dans ce cas, on observera des franges d'interfèrence.
Ainsi, l'intensité est déduite de la façon suivante:
Soit ψ1, l'onde s'étant propagée dans le bras 1: Ψ1= Ψ0.r.t.eik (αx+γz)
Et ψ2 l'onde s'étant propagée dans le bras 2: Ψ2= Ψ0.r.t.eik.D2
où: α et γ sont les cosinus directeurs dans les direction x et z: α=sin(θ) et γ=cos(θ)
r et t: les coefficients de réflexion et de transmission des séparateurs de faisceaux.
k: le vecteur d'onde.
D2: distance du chemin suivie par Ψ2.
On a alors:
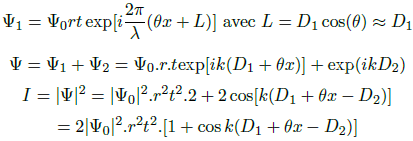
Remarque:
Lorsque θ est égale à zéro, dans l'expression ci-dessus, on voit que la dépendance en x
disparaît ainsi on se retrouve dans le premier cas, où l'intensité est uniforme dans le plan.
On peut aussi déterminer à partir des positions des maximas d'intensité, la distance entre deux franges lumineuses
ou sombres :
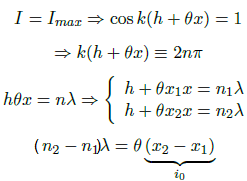
Avec n un entier relatif et k=2π/λ.
Si n2=n1+1, alors: i0= λ/θ
2-Interférences avec la lame
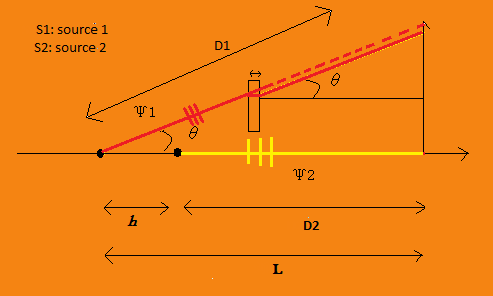
On introduit maintenant une lame d'épaisseur e dans la trajectoire du rayon Ψ1.
Le calcul se réecrit de la même façon
sauf que maintenant la trajectoire optique du rayon Ψ1 étant : D′1 = D1 + e(n-1) ,
l'expression de l'amplitude et de l'intensité totale sur l’écran d'observation deviennent :
Avec h=L - D2 =D1 - D2
et l'intensité est donnée par:
