Optimisation
Le montage tel que présenté à la page précédente ne nous a pas permis de visualiser les franges d’interférences issues de l’interféromètre. En effet, le faisceau laser a un diamètre de l’ordre de 0.5 mm et est relativement intense, donc il est délicat d’y voir des franges d’interférences. On a donc grossit le faisceau en ajoutant un télescope.
Mise en place du premier télescope
Ce télescope est constitué de deux objectifs de microscope, dont les caractéristiques sont données plus loin. Ce dispositif va nous permettre d'obtenir un faisceau grossi et collimaté.Cependant, lors de sa mise en place, nous avons rencontré certains problèmes.
1. L'injection du faisceau à l'entrée du télescope:
La source laser étant solidement fixée au banc optique, il est assez compliqué d'orienter le faisceau et de bien l'aligner par rapport aux optiques. Pour résoudre ce problème, nous avons ajouté deux miroirs à la sortie de la source laser. Grâce à ces deux miroirs, nous avons gagné en degrés de liberté. Ainsi, il est maintenant possible de jouer sur l'alignement horizontal et vertical du faisceau. Dès lors la mise en place des deux miroirs, il faut s'assurer que le faisceau et les deux objectifs du télescope soient alignés. Autrement dit, il faut que le faisceau issu du laser coïncide à la fois avec l'entrée du premier objectif et du deuxième.2.Dans le positionnement des deux objectifs:
On souhaite que le faisceau ait un diamètre de 5mm environ,
qu'il soit collimaté et que sa taille ne varie pas sur la distance utilisée dans notre étude.
Pour cela, on choisit deux objectifs dont le rapport de grossissement est de 10, ce qui donne le grossissement à la sortie du télescope.
On place donc un premier objectif de grossissement 40 suivi d'un deuxième objectif de grossissement 4.
Pour avoir à la sortie un rayon collimaté, il faut que la focale image du premier objectif coïncide avec la focale objet du deuxième.
En effet, l'image d'un objet se trouvant à la distance focale d'une lentille (ici objectif du télescope)
se forme à l'infini et a une taille constante.
Or, dans la pratique, il est impossible de se positionner à l'infini.
On se propose donc de vérifier seulement si la taille de l'image obtenue en sortie de télescope est constante sur une distance environ 3 fois plus grande (distance supposée infinie par rapport à la distance utilisée sur le banc d'optique)
que la longueur des bras du Mach-Zehnder (longueur parcourue par les faisceaux).
La figure ci-dessous illustre le positionnement de chaque objectif:
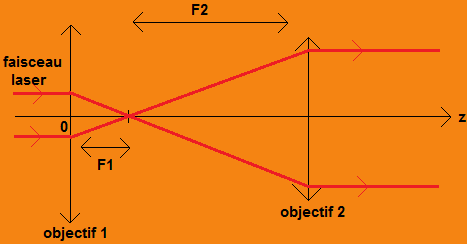
FIG 2.1: Schéma représentant le dispositif du télescope
Sur la figure(2.1), on voit qu'à la sortie du télescope (sortie du deuxième objectif) le faisceau est grossi, collimaté et de taille constante.
→ L’objectif 1 permet de focaliser le faisceau.
→ L'objectif 2 permet de collimater le faisceau avec un diamètre plus grand qu'initialement.
Dispositif expérimental
Dans cette partie, sont présentés les résultats avec le Mach-Zehnder "simple" obtenus après avoir ajouté les optiques nécessaires pour l'optimisation.

FIG 2.2: Dispositif de l'interféromètre de Mach-Zehnder optimisé
Sur la figure (2.2) sont représentés le Mach-Zehnder ainsi que les optiques ajoutées pour l'optimisation: les miroirs M'1, M'2 et le téléscope.
Les flèches rouges représentent le trajet parcouru par le faisceau. Lefaisceau incident arrive sur le miroir M1' (de coefficient de réfléxion de 100%), se réfléchit sur le miroir M'2 pour arriver à l'entrée du premier objectif du téléscope (objectif 1),
puis sur l'objectif 2 après avoir traversé un trou, permettant de "nettoyer le faisceau". Il arrive ensuite sur l'interféromètre où il va être séparé, par le BS1, en deux faisceaux secondaires qu'il faudra recombiner
ensuite sur le BS2 afin d'avoir des interférences.
Expression analytique de l'intensité
Dans cette partie, on calcul l'intensité résultante des interférences correspondant au dispositif de la figure 2.2. Pour cela, on simplifie le dispositif en considèrant les miroirs M1 et M2 comme deux sources secondaires S1 et S2 qui feront interférer les ondes Ψ1 et Ψ2 sur notre écran d’observation.
Le dispositif de l'interféromètre de Mach-Zehnder de la figure 2.2 peut se simplifier de la façon suivante :
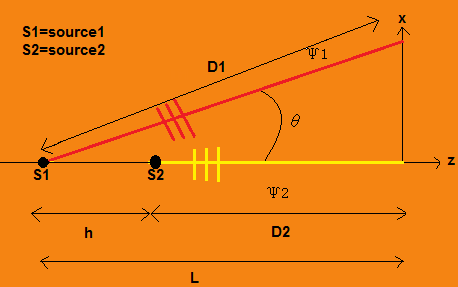
FIG 2.3: Schéma du Mach-Zehnder simplifié
I = 2 |ψ0|² (rt)² {1 + cos [k (h + θ x) ] } (2.1)
Par ailleurs, on en déduit l'interfrange: i0 = λ/θ (2.2)
avec λ la longueur d'onde et θ l’angle séparant les deux vecteurs d’onde.
Résultats expérimentaux
Une fois le dispositif mis en place, nous devons superposer les deux faisceaux à la sortie de celui-ci, c'est à dire sur le séparateur de faisceau (BS2) et sur la caméra.
Les deux faisceaux étant:
→faisceau1 = faisceau se propageant sur le bras 1;
→faisceau2 = faisceau se propageant sur le bras 2.
Pour cela, nous devons jouer, à la fois, sur le miroir M1, le miroir M2 et le BS2.
Le miroir M1 va déplacer le faisceau 2, verticalement et horizontalement sur le BS2, alors que le miroir M2 va déplacer le faisceau 1.
On fait ces manipulations jusqu'à observer une superposition optimale sur la caméra.
Voici les résultats obtenus:
1)Résultats avant optimisation :
Sur la figure 2.4, sont représentées les interférences obtenues avant l'ajout d'un trou entre les deux objectifs du télescope. La figure 2.5 représente une coupe de l'intensité.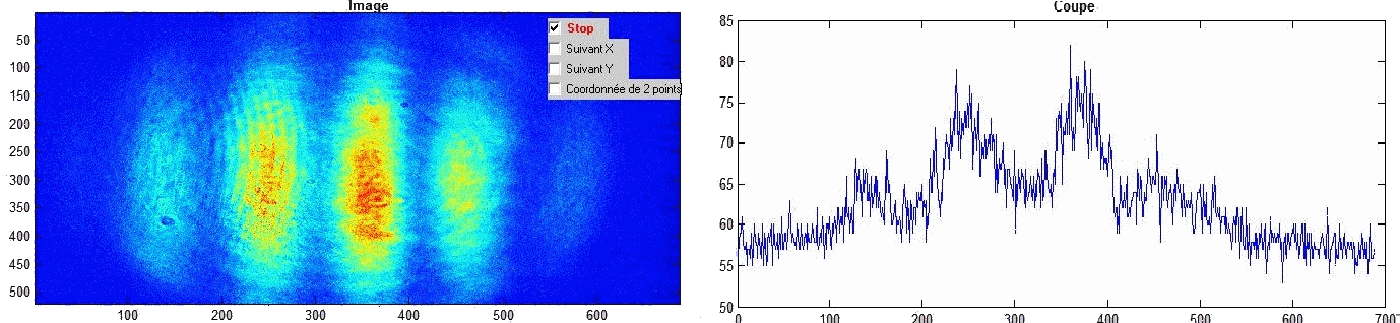
Nous allons donc ajouter un trou, de diamètre de quelque micron environ, que l'on va placer entre les deux objectifs.
2)Résultats après ajout du trou :

On visualise les interférences à l'aide d'une caméra placée en sortie du dispositif, c'est à dire après le séparateur de faisceau BS2.
La caméra nous permet d'observer directement les figures d'interférences (figure 2.6).
On traite ensuite la figure à l'aide d'un logiciel Matlab, on obtient ainsi la figure (2.7).
D’après l'expression (2.2), on voit que l’interfrange dépend seulement de la longueur d’onde λ, et de l’angle θ séparant les deux vecteurs d’onde.
Afin de valider cette expression, on se propose dans la partie suivante de réaliser la même manipulation mais en ajoutant une lame d'épaisseur e sur l'un des bras du dispositif.
