Interférences avec fibre:
Après avoir optimisé au maximum les interférences avec le Mach-Zehnder simple et après s'être familiarisé avec les réglages expérimentaux, on passe à l'étape qui nous intéresse: ajout de la fibre optique. Cependant, nous rencontrons certains problèmes:
Dispositifs:
Aprés s'être affranchi des problèmes rencontrés lors de la mise en place de la fibre, nous présentons ici le dispositif:
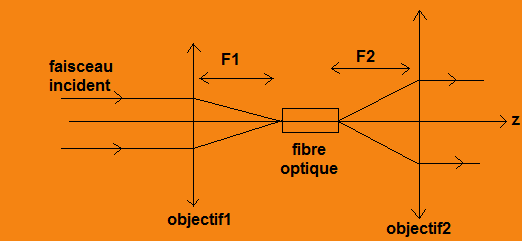
FIG 4.1: Schéma représentant le dispositif de la fibre avec les 2 objectifs
Sur ce schéma, est représenté l'emplacement de la
fibre, afin visualiser l'image de l'intensité à la sortie.
Objectif 1: grossissement de 3,5
Objectif 2: grossissement de 20.
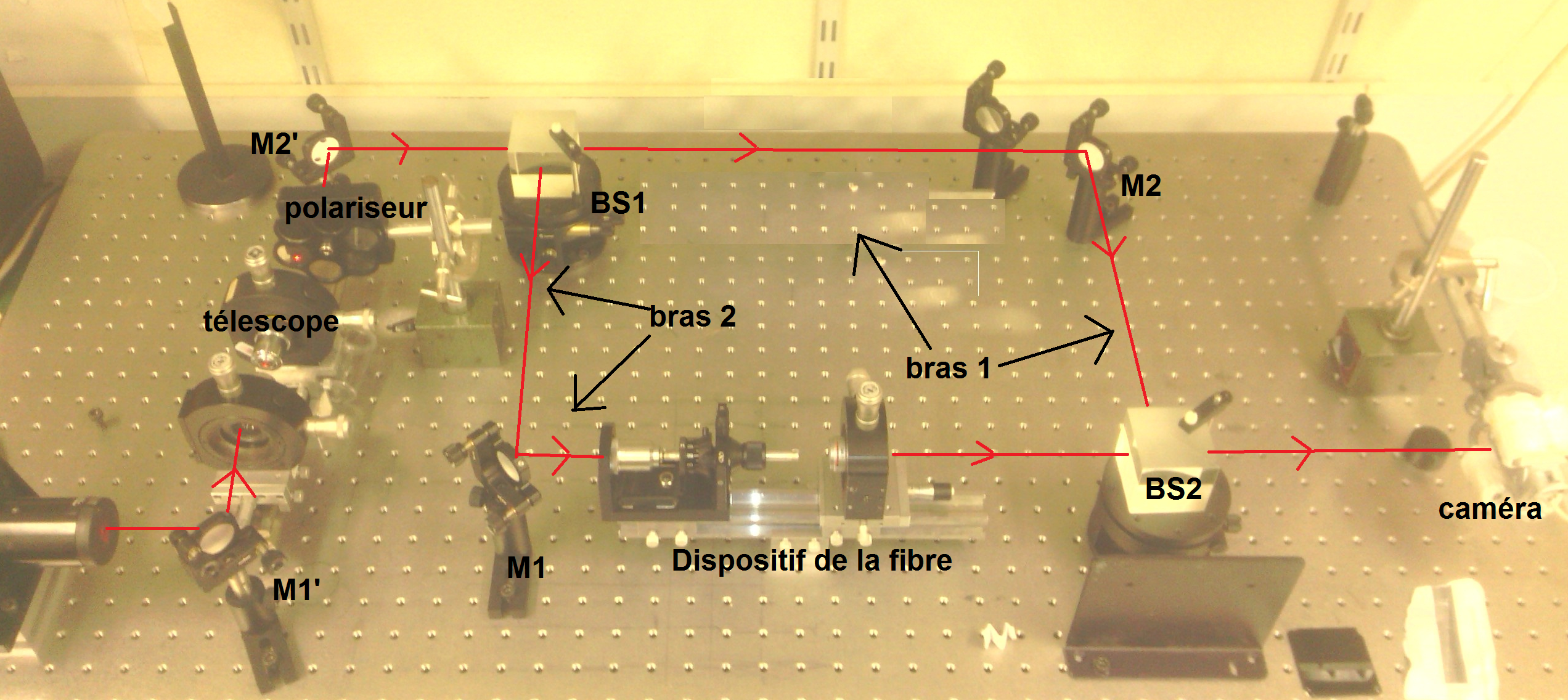
FIG 4.2: Dispositif expérimental avec fibre et téléscope
Sur ce schéma, on représente l'interféromètre de Mach-Zehnder ainsi que la fibre et le téléscope correspondant.
La fibre utilisée ici est une fibre optique multimode, de longueur 8 cm et de diamètre 125µm.
Les flèches rouges correspondent au trajet pacouru par le faisceau.
Résultats obtenus:
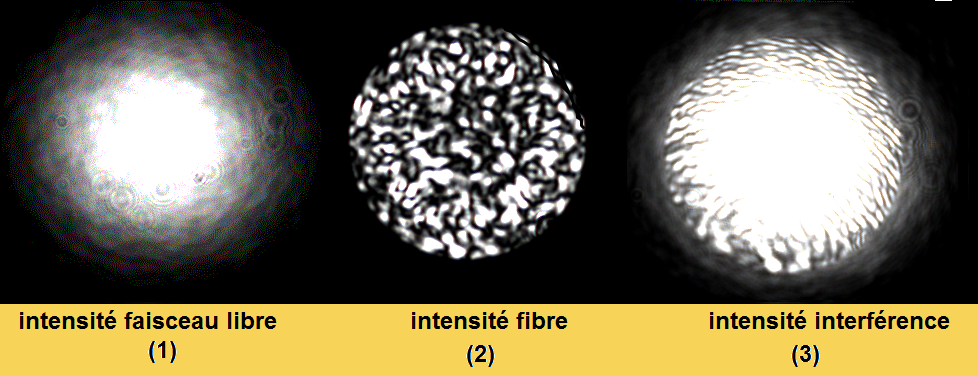
FIG 4.3: Figures représentants les résultats obtenus avec la fibre
Observations:
Sur la figure ci-dessus, est représentée l'intensité du faisceau libre secondaire (intensité faisceau libre(1)), l'intensité sortant de la fibre (intensité fibre(2)) et la superposition de ces deux intensités (intensité interférence (3)).
On remarque que l'intensité du faisceau libre n'est pas uniforme: on a une tâche centrale très intense, correspondant au lobe central de la gaussienne (faisceau libre qui possède un maximum d'intensité à ce niveau), et un contour moins intense.
Ceci a une conséquence sur la répartition de l'intensité résultante de la superposition de la gaussienne avec l'onde issue de la fibre. En effet, on voit sur la photo 3 de la figure 4.3 que l'intensité est plus intense au centre que sur les contours.
Pour avoir des résultats optimisés au maximum pour la phase, on va grossir la tâche centrale du faisceau de façon à ce qu'elle englobe tout le faisceau sortant de la fibre. Ceci revient donc à grossir tout le faisceau libre.
Solutions:
- soit grossir le faisceau principal, (faisceau se trouvant avant le BS1) en changeant l'une des deux lentilles du premier télescope. Dans ce cas, il faudrait refaire tous les réglages et les alignements de nouveau;
- soit ajouter un nouveau télescope qui grossit le faisceau libre secondaire (faisceau se propageant sur le bras 1), avant que ce dernier n’interfère avec faisceau issu de la fibre.
On choisit la deuxième option. En effet, cela nous dispense de refaire tout le montage dans la mesure où on n'aura à modifier que les réglages des optiques du bras libre 1 (la partie du montage où l'on place le télescope).
On place donc un nouveau télescope, entre le séparateur (BS1) et le miroir (M2), composé de deux objectifs conjugués : le premier ayant un grossissement de 20 et le deuxième de 10. On aura donc un faisceau deux fois plus grand.
Pour l'emplacement des objectifs, on effectue la même procédure que pour le premier télescope.
Nouveau dispositif:

FIG 4.4: Dispositif expérimental avec fibre et ces deux objectifs correspondant
Légende:
1: Téléscope 1 (objectifs de grossissement:40 et 10)2: Polariseur
3: Séparateur de faisceau (BS1)
4: Télescope 2: (objectifs de grossissement 20 et 10)
5: Miroir M2
6: Séparateur de faisceau (BS2)
7: Dispositif de la fibre (de gauche à droite: objectifs de grossissement 20 puis de 3,5)
8: Miroir M1
9: Caméra
Résultats obtenus:

FIG 4.5: Figures illustrants les résultats obtenus après la mise en place du téléscope
Observation:
De là, se pose la question : Comment extraire la phase accumulée par le faisceau issu de la fibre optique à partir des observations de la figure 4.5 ?
On se propose donc de détailler le calcul aboutissant à l'expression analytique de la phase à partir de l'intensité.
Calcul de la phase à partir des données expérimentales:
Soit l'expression analytique de l'onde libre: |ψ1|.eikh , avec |ψ1| l'amplitude complexe de l'onde optique s'étant propagée sur le bras 1 et h la distance du chemin suivi par l'onde libre.
On sait que l'expression de l'onde, se propageant dans une fibre, correspondant à un mode de propagation est de la forme:
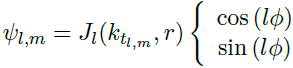 (4.1)
(4.1)2l : nombre de zéros du champ suivant la coordonné azimutale
m-1 : nombre de zéros du champ suivant la coordonnée radiale
lΦ : la phase de l'onde se propageant dans la fibre.
L'expréssion (4.1), représente le champ d'un seul mode de propagation. Pour une fibre multimode, le champ issu de la fibre est une superposition de plusieurs modes de propagation.
Il s'écrit analytiquement: 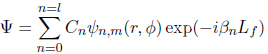 (4.2)
(4.2)
avec
βn : les constantes de propagation pour le mode
Lf : la longueur de la fibre
Cn: le point du mode n dans la superposition.
D'où, en remplaçant dans l'expression (4.2) ψn,m par son l'expression donnée en 4.1 et en posant Ψ=ψ2 , on a:
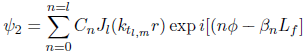 (4.3)
(4.3)avec nΦ : la phase correspondant à un mode de propagation n.
On en déduit donc l'intensité résultante de l'interference entre ψ1 et ψ2 : I=|ψ1 + ψ2|2
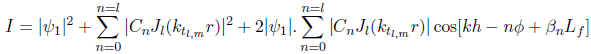 (4.4)
(4.4)On peut remarquer que l'expression (4.4) est assez complexe, il nous est donc très difficile de remonter de cette façon à la phase. Si on reprend l'expression de ψ2, on peut simplifier son écriture de la façon suivante:
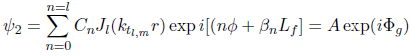 (4.5)
(4.5)Où Φg, représente la phase globale à la sortie de la fibre. En effet, étant donné que, mathématiquement, la somme de nombres complexes est un nombre complexe, on peut se permettre la simplification ci-dessus.
D'où, en remplaçant |ψ1| par B et |ψ2| par A, dans l'expression (4.4), on en déduit:
L'expression analytique de la phase résultante s'écrit donc:
On a donc une équation qui lie la phase de l'onde dans la fibre (Φg) à l'intensité du faisceau libre (B2), l'intensité du faisceau traversant la fibre (A2), l'intensité résultante des interférences (I) et la phase accumulée par le faisceau libre (kh).
On traite ensuite les images de la figure 4.5 à l'aide d'un code Matlab (fourni par nos encadrants). Celui-ci va"en gros"appliquer l'équation 4.4 et en sortie imager la phase.
Sur la figure suivante, sont représentés les résultats obtenus après traitement:
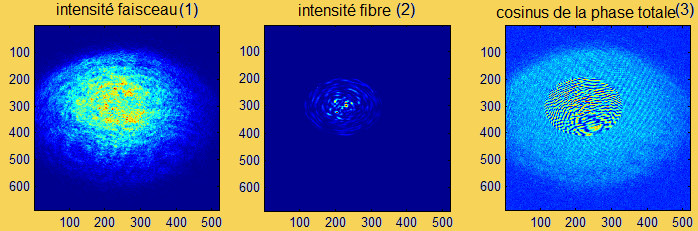
FIG 4.6: Figures illustrants les résultats obtenus après traitement Matlab
Remarque: Sur la photo (3) de la figure 4.6, est représenté le cosinus de la phase totale: kh - Φg,
c'est-à-dire la phase accumulée par le faisceau libre à laquelle on soustrait la phase accumulée par le faisceau issu de la fibre.
Code couleur: sur l'image 3 ("cosinus de la phase totale"), la couleur rouge correspond à une phase égale à π et la couleur bleue correspond à une phase nulle.
Remarque: Dans la suite, les acquisitions sont obtenues avec une webcam de moins bonne résolution.
1)Rotation de la fibre:
On réalise une rotation de la fibre autour de son axe. En faisant cela, on excite d'autre mode de la fibre.Voici les résultats obtenus: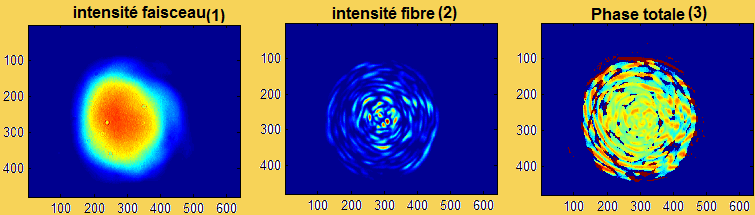
FIG 4.7:Figures illustrants les résultats obtenus aprés rotation de la fibre
2)Dés-centrage du faisceau libre:
On fait bouger le faisceau libre, à l'aide du miroir M2 et du BS2, de façon à ce que celui-ci ne se supperpose pas totalement sur le faisceau issu de la fibre. Voici les résultats obtenus:
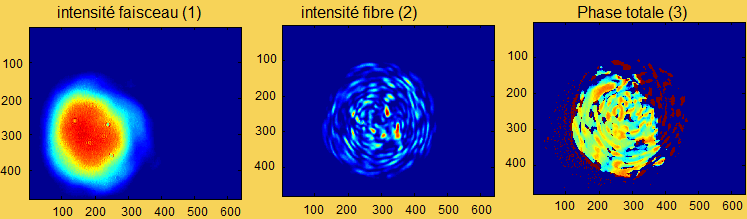
FIG 4.8: Figures illustrants les résultats obtenus aprés dés-centrage du faisceau libre
Lorsqu'on décentre le faisceau libre, il n'englober qu'une "partie" du faisceau issu de la fibre. Ceci va avoir une conséquence sur la phase totale due aux interférences. En effet, l'image de la phase sur la photo 3 peut être décomposée en deux parties:
-Une première, de couleur jaune-bleu: la phase, imagée sur celle-ci, résulte de la superposition des deux faisceaux (libre et issu de la fibre). Cette phase correspond donc à la somme de la phase du faisceau libre et du faisceau issu de la fibre.
-Une deuxième, de couleur rouge: la phase imagée sur celle-ci, correspond à un résidu d'interférences, inexploitable.
Conclusion:
Grâce à l'interféromettre de Mach-Zehnder, nous avons réussi à imager la phase d'une onde à la sortie de la fibre optique.
Nous avons ensuite vu les conséquences d'un mauvais réglage sur l'image de la phase (dés-centrage du faisceau libre).
Afin de valider le protocole inteféromètrique qui nous a permis de déterminer la phase d'une onde se propageant dans une fibre, on souhaite comparer nos résultats expérimentaux à ceux qu'on peut obtenir en effectuant une simulation numérique.
