

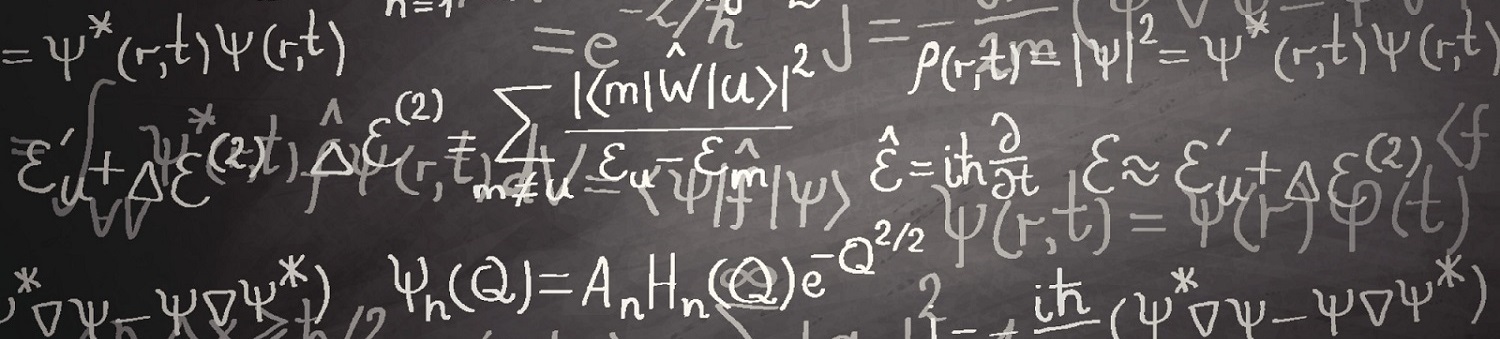

Dans cette partie nous allons rendre compte des résultats obtenus à l'aide de notre programme pour le potentiel harmonique :  .
.
Ainsi, nous pourrons vérifier si notre programme fonctionne correctement. Nous avons commencé par vérifier la convergence des énergies en fonction de la dimension de la matrice générée (N est la taille de la matrice du hamiltonien).
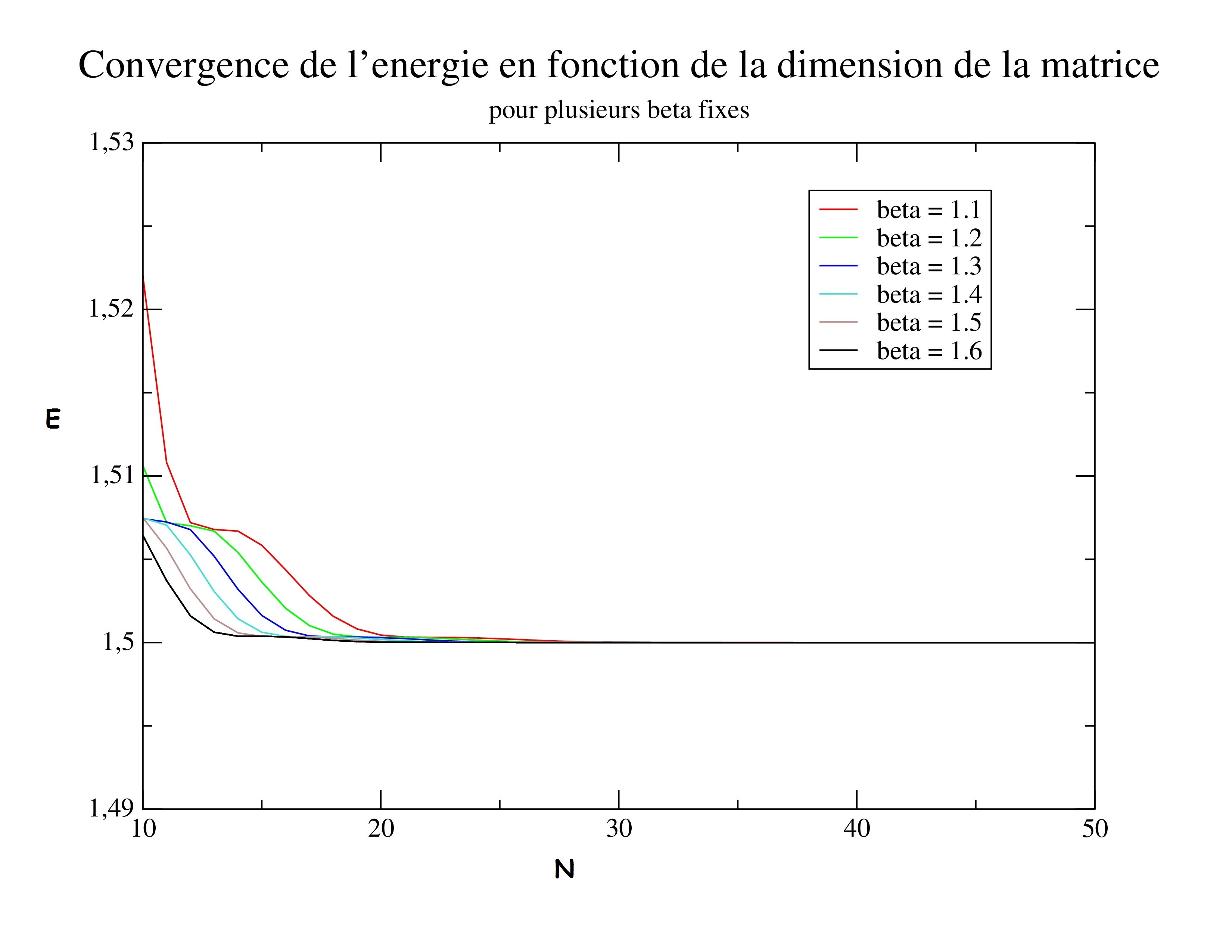
Sur ce graphe, nous avons tracé l'évolution du premier niveau d'énergie en fonction de la dimension du système. Tout le long de notre étude, nous avons adopté une méthode dite variationnelle. Cette méthode nous permet de savoir que toute énergie trouvée avec une matrice de dimension N sera supérieure à la vraie valeur trouvée pour une matrice de dimension infinie. Les énergie convergent donc vers une valeur fixe quand la dimension de la matrice augmente.
A partir des valeurs propres calculées par notre programme, nous avons reconstitué le graphe rendant compte des différentes valeurs propres d'un système soumis au potentiel harmonique. Cliquer ici
Bien que cette première vérification suffise à montrer que notre programme fonctionne, nous avons toutefois représenté les fonctions d'ondes liées à ce potentiel pour comparer leur allure à l'allure théorique.Cliquer ici