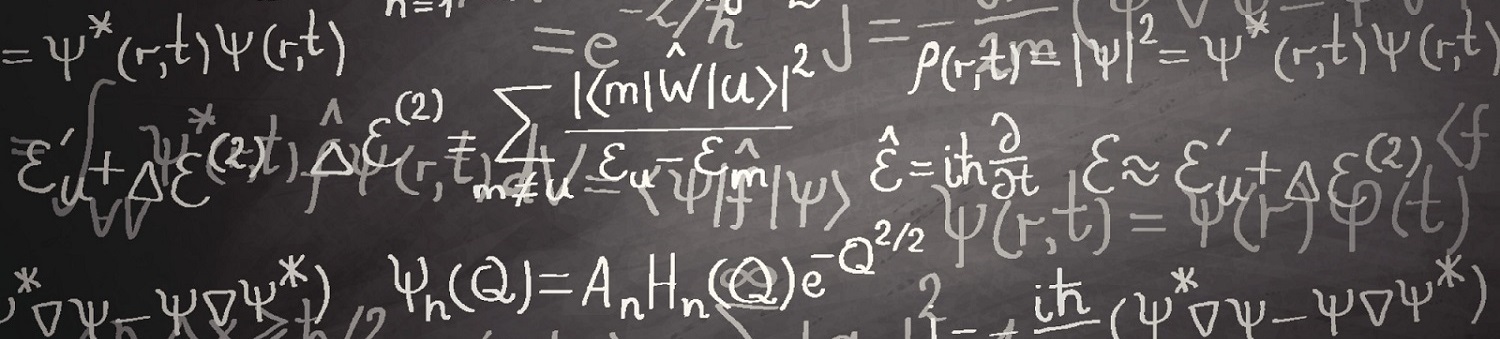
L'espace de Hilbert dans lequel le système se trouve est de dimension infinie. Il faut donc théoriquement pour le hamiltonien une matrice de taille infinie. Pour avoir un programme fonctionnel avec une matrice de dimension finie il faut donc une base pertinente. Une bonne base pour cela est la base des polynômes de Laguerre.
On définit les paramètres suivants : r la distance entre les particules, 
la composante angulaire et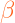 
un paramètre numérique d'échelle.
L'idée est de projeter la base des polynômes de Laguerre dans la base réelle : 
Après vérification on obtient bien une matrice unitaire (preuve que la base est normalisée).
Nous avons calculé la matrice de l'énergie cinétique et celle de l'énergie potentielle, puis la matrice du hamiltonien par la relation : 
Nous avons testé ce programme sur le potentiel harmonique dont les énergies des états liés et les fonctions d'ondes sont connues. Pour voir les résultats cliquer ici.
Les résultats pour le potentiel étudié sont ici.