


Dans cette partie nous allons expliquer les résultats obtenus pour le potentiel de notre étude : 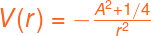 .
.
Nous allons dans un premier temps, comme pour le potentiel harmonique, tracer les énergies calculées en fonction de la dimension de la matrice. Comme nous suivons une méthode variationnelle nous devrions constater qu'ici aussi on a une convergence des énergies avec l'augmentation de la dimension de la matrice, la valeur la plus petite étant la valeur la plus juste. On pourra ainsi définir une taille minimale de notre matrice pour laquelle l'étude nous donnera les résultats les plus proches de la réalité.
Ici nous avons étudié la convergence de l'énergie de l'état fondamental en fonction de la dimension de la matrice :
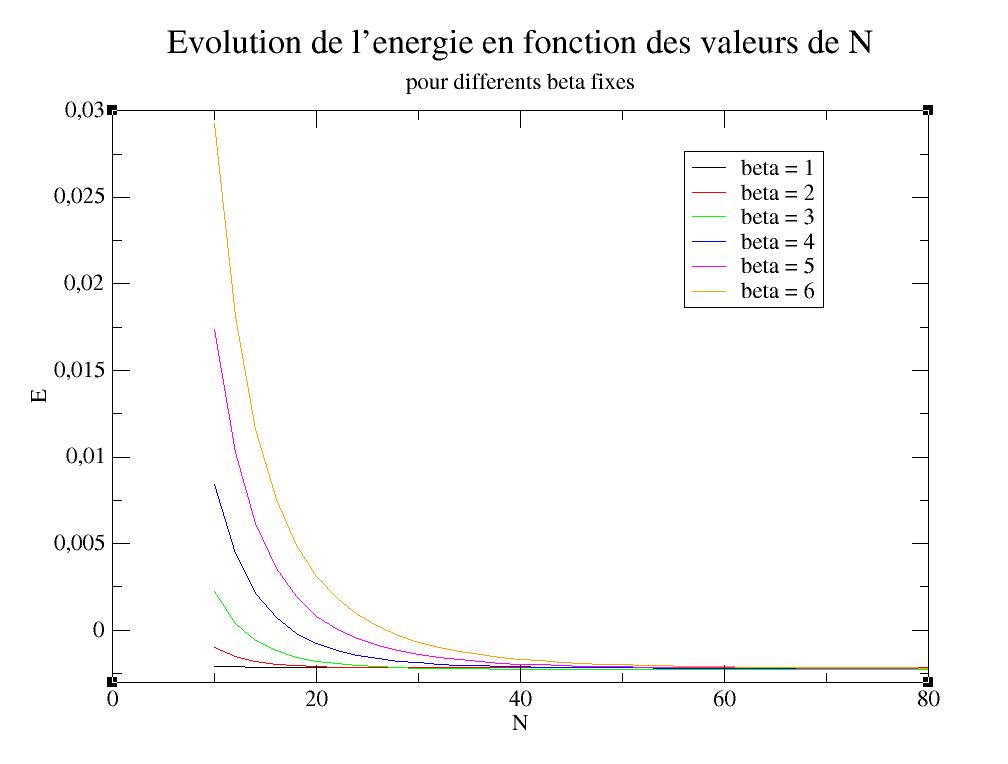
On a comme pour le potentiel harmonique représenté les énergies des états liés sur le graphe du potentiel ici.