Le champ électrique
Il faut qu’il soit suffisamment élevé pour vaincre les forces thermiques dues au mouvement Brownien, qui tend à casser les « colonnes » formées. Le paramètre d’échange, de par sa dépendance en E2, gouverne tout le système puisque la valeur du champ électrique détermine la création des « colonnes ». On a alors :
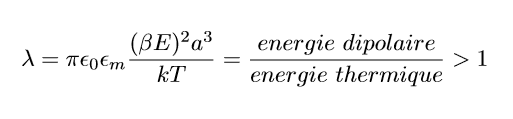
Expérimentalement, nous devons donc chercher la valeur du champ limite Elim pour lequel la création de colonnes est effective.
Pour déterminer cette valeur, nous réalisons une première manipulation, dans laquelle nous fixons la fréquence à 5 Hz, en faisant varier la valeur du champ électrique de 0 à 2500 V/mm.
Comme expliqué précédemment, nous suivons l’avancée du processus de formation du réseau de colonnes, à l’aide d’un rhéomètre. Celui que nous utilisons est couplé avec des électrodes permettant d’imposer un champ électrique. Il est alors possible faire varier les valeurs de champ et de fréquence appliquées au système entre les électrodes au cours du temps.
Nous obtenons le graphe suivant, représentant G’ et G’’ en fonction du temps retraçant l’historique des mesures effectuées :
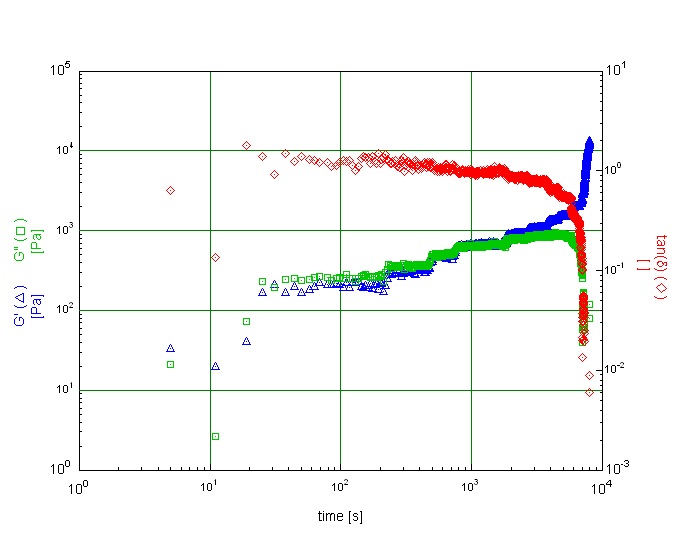
Ici, G’ représente le module élastique et G’’ le module de perte.
Quand on observe G’> G’’, la création de colonnes est plus importante que leur destruction, au contraire si G’ < G’’, alors la plupart des colonnes formées se cassent. Toutes les colonnes sont cassées quand G’ est nul.
Ainsi, grâce aux valeurs de champ relevées, combinées aux valeurs du module élastique, nous traçons le graphe de G’ en fonction de la valeur du champ électrique appliquée.
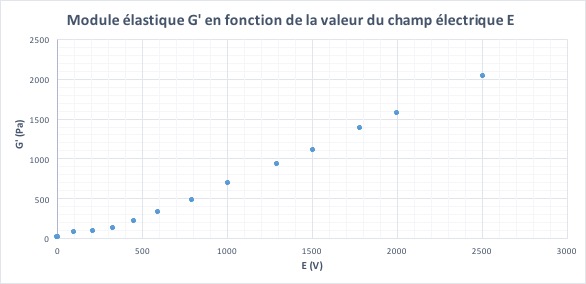
Pour définir les domaines de formation d’un réseau de colonnes, nous utiliserons 3 critères :
- la valeur du paramètre d’échange λ >> 1,- la présence d’un module élastique G’ non nul,
- le facteur de perte : tan δ = G’’/G’ << 1 (en rouge sur le graphe 1).
Nous pouvons observer que, pour un champ faible, G’ est très faible et évolue peu, indiquant qu’il n’y a pas de « colonnes » formées dans le système. Puis à partir d’une certaine valeur, G’ augmente fortement, indiquant la formation de « colonnes ». Cette valeur limite, que l’on notera Elim, correspond donc au champ minimum nécessaire au système pour qu’il y ait une formation effective de « colonnes ».
En effet, elle permet de satisfaire la condition imposant à l’énergie dipolaire d’être supérieure à l’énergie thermique, en d’autres termes que le paramètre d’échange soit supérieur à 1, c’est-à-dire
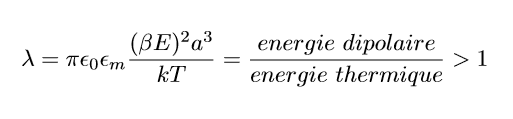
Nous pouvons donc en déduire que pour des valeurs inférieures à Elim, le champ électrique ne fournit pas assez d’énergie au système pour former des «colonnes» complètes mais assez pour former des agglomérats, le module élastique n’est donc pas nul. Le système est, alors, sous forme d’une suspension viscoélastique (tan δ >> 1). Puis au dessus de cette valeur, le système reçoit suffisamment d’énergie pour former des colonnes complètes : le système forme un réseau de colonnes. (voir graphe 3)
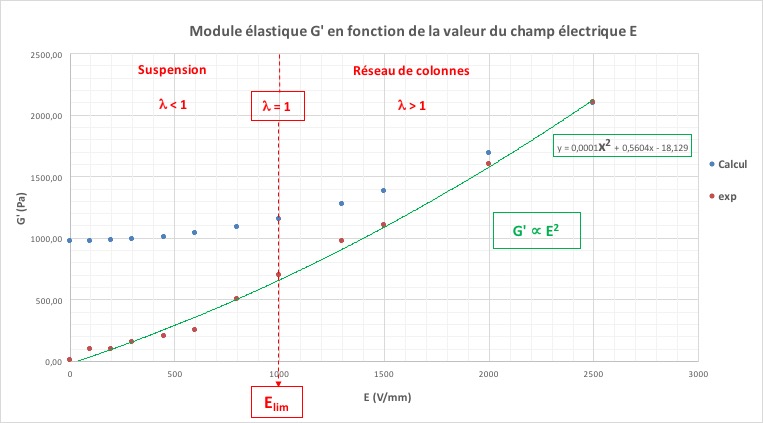
Expérimentalement, la valeur limite du champ correspond au changement brutal de pente du graphe 3. Nous obtenons, graphiquement, que la valeur du champ limite est Elim = 1000 V/mm.
Pour comparer avec la théorie, nous réalisons le calcul avec nos valeurs et traçons également la courbe théorique sur le graphe 3 (voir Annexe : complément sur le calcul théorique du module élastique G’, pour l’explication détaillée des calculs).
De plus, le PDMS étant considéré comme un diélectrique pur, nous allons montrer que la formule du paramètre d’échange, suivante, s’applique à notre fluide ER :
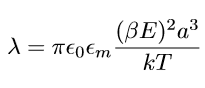
Nous pouvons vérifier cela en insérant une régression polynomiale sur le graphe du module élastique G’ en fonction de E. Nous obtenons bien une courbe de type polynôme du second degré et nous pouvons donc dire qu’à partir de Elim, le module élastique G’ est proportionnel au carré du champ électrique comme le prévoit le modèle dipolaire.
En effet, sur le graphe 3, pour λ >> 1, les valeurs de G’ expérimentales et calculées sont de même ordre de grandeur, validant donc le modèle théorique qui suppose des interactions dipolaires.
La fréquence
Il nous faut, à présent, trouver l’intervalle de fréquence correspondant au mécanisme de polarisation des particules de TiO2, permettant à la polarisation d’être effective et ainsi d’aligner les particules créant un réseau de colonnes.
Expérimentalement, nous réalisons une manipulation dans laquelle nous fixons la valeur du champ électrique à 1000V/mm, en faisant varier la fréquence entre 5 et 2000 Hz.
Sur le graphe 4, on obtient un graphe de G’ et G’’ en fonction du temps qui retrace l’historique des mesures effectuées :
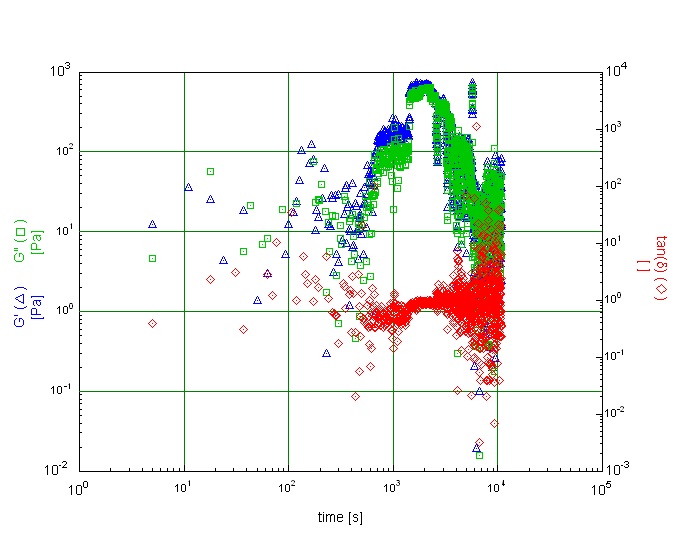
De même que précédemment pour le champ électrique, nous traçons, cette fois, le graphe du module élastique G’ en fonction de la fréquence (voir graphe 5).
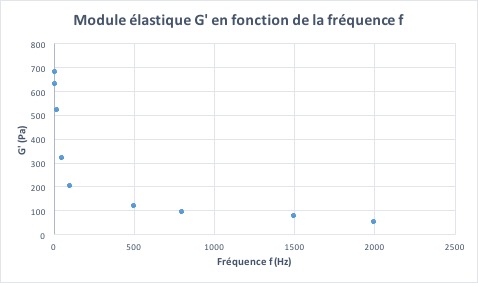
Nous observons que plus la fréquence augmente, plus le module élastique diminue, allant jusqu’à quasiment s’annuler. Ceci traduit donc le fait que, pour des valeurs de fréquence très élevées, le nombre de colonnes détruites est plus important que celui de colonnes construites.Nous pouvons donc en conclure que, pour assister à la formation du réseau de colonnes, nous devons appliquer de faibles fréquences au système. C’est-à-dire, des fréquences non nulles (pour éviter l’électrophorèse) d’une dizaine de Hertz.
De plus, pour en déduire le type de mécanisme de polarisation des particules de TiO2, nous utilisons le graphe ci-dessous (graphe 6). Représentant la valeur de la constante diélectrique du milieu en fonction de la pulsation (reliée à la fréquence par ω = 2πf), il nous indique les différents types de polarisation selon la fréquence appliquée. Il est à comparer à notre graphe expérimental.
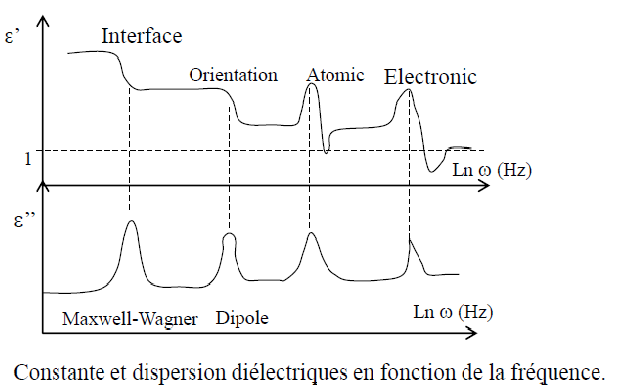
ε’ est la constante diélectrique du milieu. On peut la relier à G’ par le fait que, G’ dépend de β (dans formule de l’énergie d’interaction) qui, elle-même, dépend de la constante diélectrique du milieu. Il est donc possible de comparer ce graphe à celui que nous obtenons.
Pour avoir un module élastique G’, il faut une énergie attractive (ayant pour but de relier le réseau de colonnes) ; ce sera l’énergie dipolaire donnée par la polarisation des particules de TiO2. Or la polarisation de TiO2 dépend de la fréquence et sera maximale pour celle correspondant au mécanisme de polarisation. Sur notre graphe expérimental, le maximum de G’ se trouve pour des basses fréquences. En comparant au graphe théorique dans le domaine des faibles fréquences, nous en concluons que le mécanisme de polarisation est un mécanisme d’interface (par migration d’impuretés à la surface de TiO2).
Nous pouvons, enfin, confirmer ces résultats par un résonnement complémentaire. En effet, nous avons compris que pour permettre la formation du réseau de colonnes, il faut satisfaire : λ > 1. Il faut donc β >1 et donc il faut que εp soit très grand devant εm. εp étant représenté par ε' sur le graphe, on remarque que le maximum de ε' correspond au mécanisme d’interface.
En conclusion, pour assister à la formation du réseau de colonnes au sein du système, il faut appliquer à celui-ci, un champ électrique assez élevé pour satisfaire à la condition que l’énergie dipolaire soit plus grande que l’énergie thermique (lutte contre le mouvement brownien). Il faut de plus se placer à basses fréquences pour que les particules de TiO2 se polarisent correctement.