Nous nous consacrerons dans cette section à l’étude de deux fermions indépendants piégés dans un puits de potentiel. Il s’agit d’un des cas les plus simples qu’il est possible d’étudier. Ainsi, nous aurons à la fois l’occasion de vérifier le bon fonctionnement de l’algorithme de Monte-Carlo Metropolis, en effectuant des analyses qualitatives et quantitatives, et nous pourrons évoquer les quelques difficultés et/ou limites qu’il faudra résoudre afin de passer à l’étude de plusieurs corps.

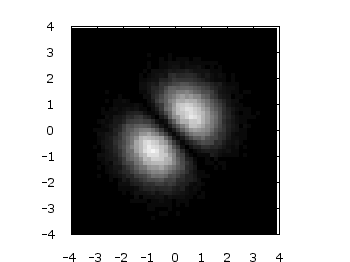
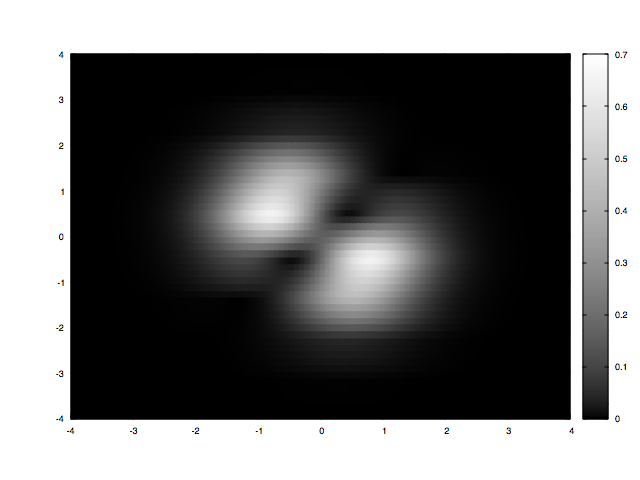
Après avoir élaboré le programme permettant de modéliser le problème, on veut s’assurer que tout marche au mieux. Dans cet objectif, on peut par exemple demander à la machine de nous donner des indices qualitatifs sur ce qu’elle est en train de calculer.

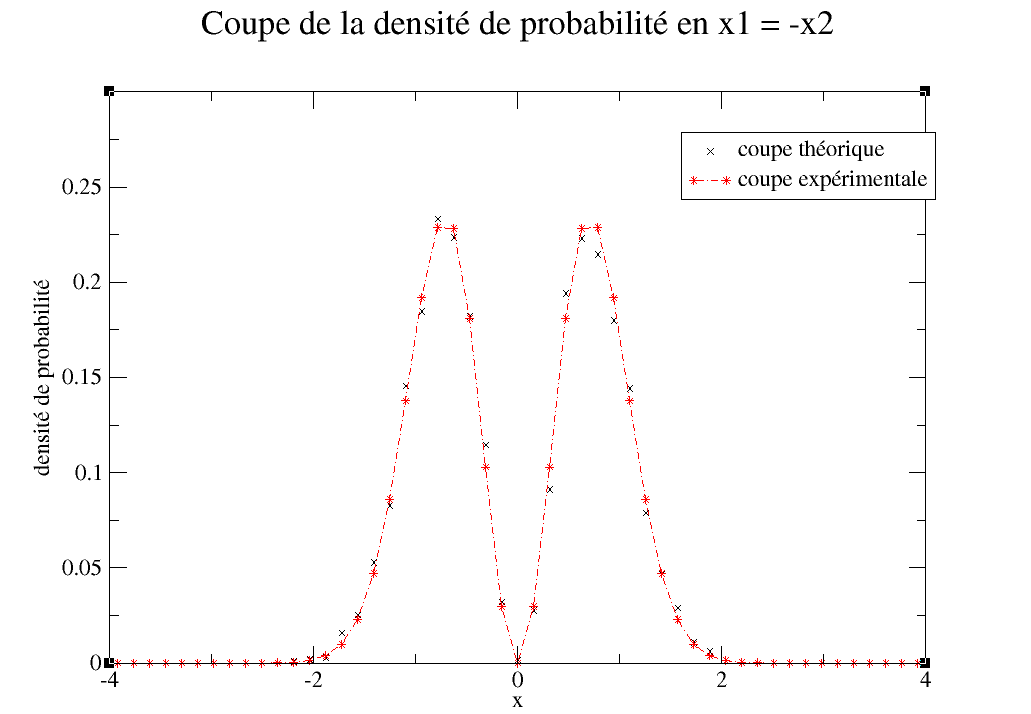
Le programme à l’air de fonctionner correctement, nous voilà rassurés. Néanmoins, il ne faut pas négliger l’importance de l’aspect quantitatif, car nous n’avons pour lors aucun moyen de savoir si nous sommes dans les bonnes échelles de mesures ! Nous décidons de tracer la coupe de la probabilité en x1 = -x2, et de comparer les points théoriques et expérimentaux en les superposant :

Le graphique ci-dessus montre que la simulation n’est pas en total accord avec les résultats théoriques. Deux points sont à noter :

• Le nombre d’itérations effectuées dans cette modélisation n’est de l’ordre que de quelques milliers, il est donc normal que les points ne soient statistiquement pas très précis.
• Nous n’avons aucune information en ce qui concerne les incertitudes statistiques des points expérimentaux ; toute comparaison avec la théorie est donc vaine.

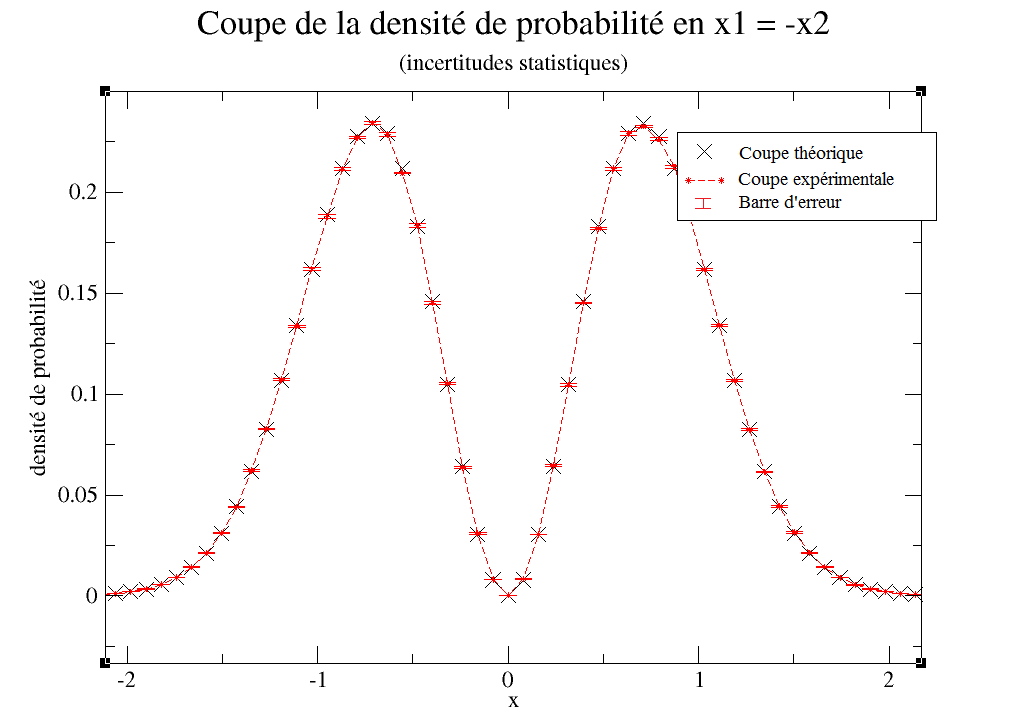
Il nous faut mettre en œuvre un morceau de code qui calcule ces incertitudes en fonction du nombre d’itérations, sachant que plus l’on collecte de configurations, plus la simulation sera précise.

Nous lançons, pour gagner en précision, une acquisition assez longue avec cent million nouvelles configurations proposées. Voici le résultat :

L’incertitude moyenne sur les points expérimentaux est de 0.49%, ce qui est relativement faible. On est désormais bien sûr que le programme ne dysfonctionne pas.

La Thermalisation

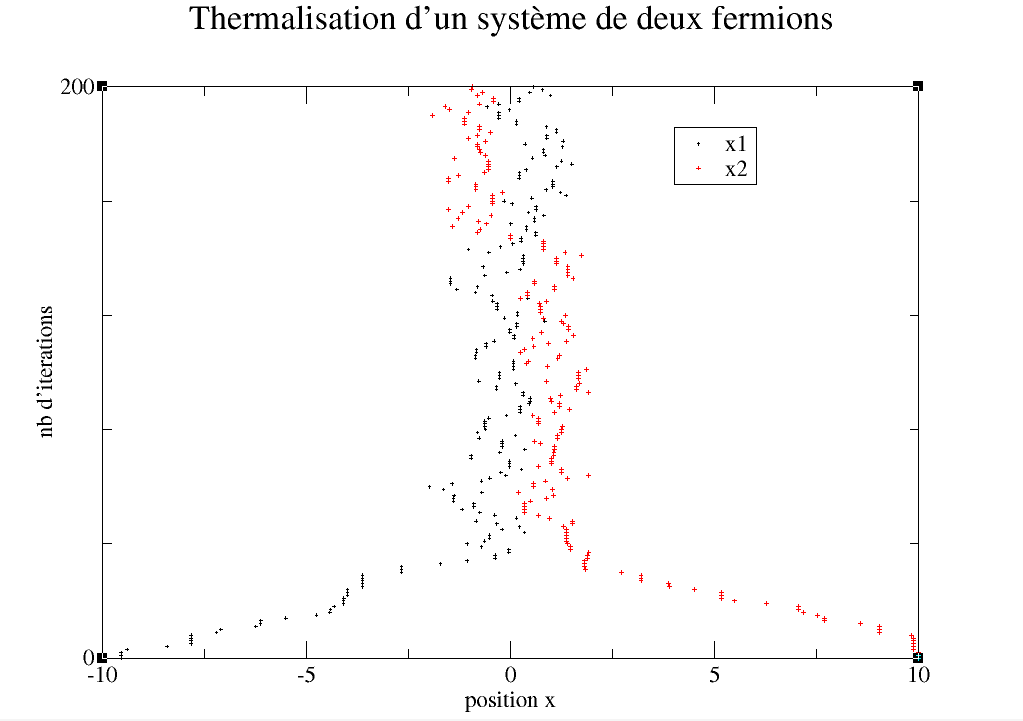
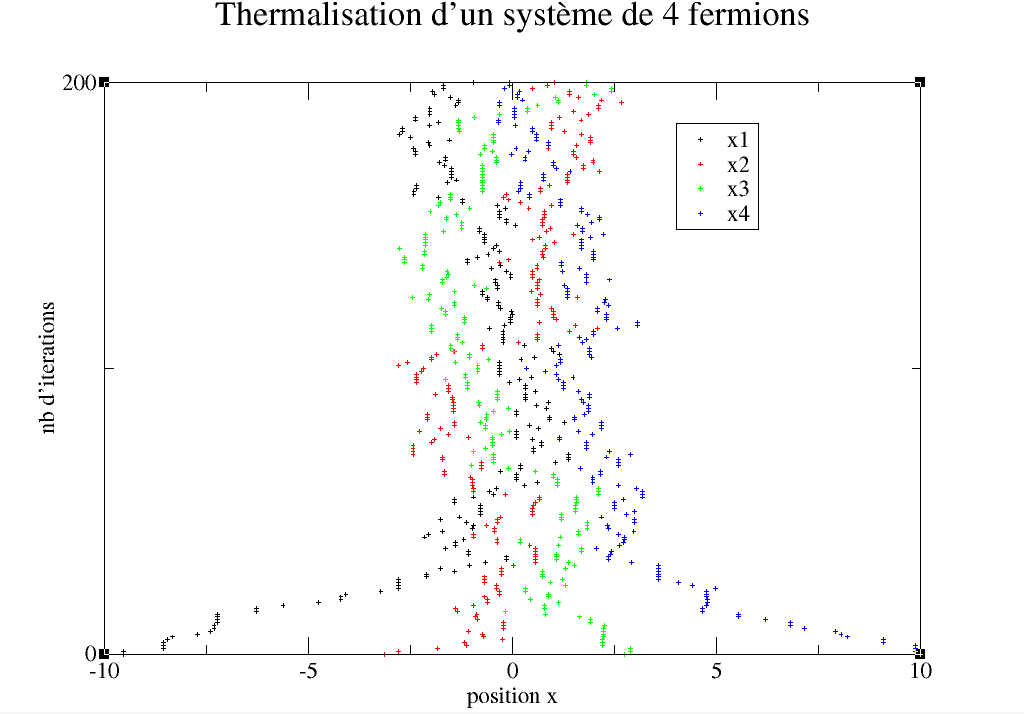
Un problème pourrait nous être objecté : il est fort possible que nos mesures soient biaisées par la configuration initiale que nous imposons arbitrairement. Il se peut que les premières mesures collectées par l’ordinateur ne rendent pas vraiment compte de la situation. Il convient donc de laisser un temps sans prises de mesures à l’algorithme : on parle de thermalisation. Nous décidons de réaliser un graphique qui témoigne de ce phénomène, dans le but de repérer l’impact réel sur nos résultats.

Si on choisit des conditions initiales très excentrées des positions les plus probables, on observe bien un temps de transition. Prendre en compte ces mesures ne ferait que fausser un peu plus la simulation numérique.

On pourrait donc être tenté par le fait d’imposer des conditions initiales proches de l’état permanent, cependant, il faudrait adapter ces conditions selon le nombre de particules.

Afin de se dispenser de mécanismes plus complexes, nous jugeons suffisant de ne débuter les mesures qu’à partir de 10% des itérations totales. Si nous faisons 1000 répétitions par exemple, seules les 900 dernières seront prises en compte.

La corrélation des mesures

Au fil de notre travail, nous réalisons qu’un autre problème peut se poser. À chaque itération, on propose une nouvelle configuration et l’algorithme l’accepte ou non, selon les règles du bilan détaillé. C’est en inspectant les mesures des configurations consécutives que nous nous apercevons d’une forte corrélation entre elles. Ainsi, la nouvelle configuration adoptée par le programme à chaque étape dépend fortement de la précédente, ceci pouvant aussi biaiser nos résultats. Nous estimons nécessaire de prendre la mesure d’une nouvelle configuration toutes les 10 itérations, afin de préserver une bonne simulation.

On remarque que le nombre de prises de mesures devient alors très faible si on le compare au calcul réel de la machine. En conséquence, seules 9% des configurations proposées par l’ordinateur sont pris en compte (thermalisation comprise).