Fonctions d'ondes

Notre objectif principal est de modéliser numériquement la répartition des bosons et fermions au sein d'un puits de potentiel. Pour le mener à bien, il est nécessaire d'avoir accès à la probabilité d'une certaine configuration des particules dans le piège harmonique. Qui dit probabilités, dit fonctions d'ondes, puisque la probabilité d'une configuration est donnée par le module au carré de la fonction d'onde correspondante. Il devient donc indispensable de les connaître selon le type et le nombre des particules étudiées.

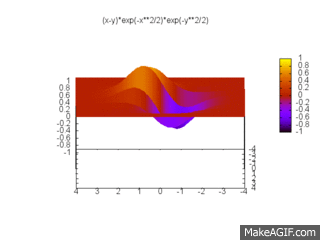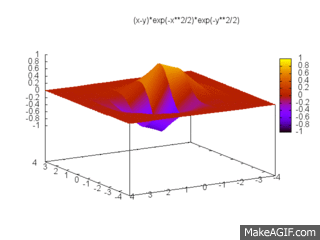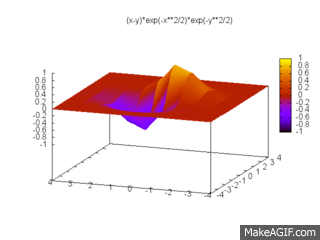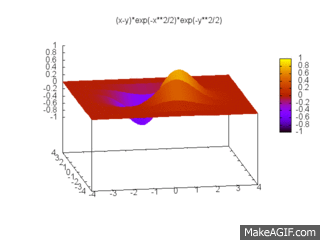
Pour deux fermions indépendants, la fonction d'onde s'écrit :

respectant l'antisymétrie et le principe d'exlusion de Pauli imposés par sa famille. C'est une fonction à deux dimensions que l'on peut tracer :

La probabilité en lien avec une certaine configuration s'écrit :

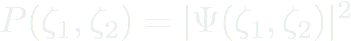
On peut tracer cette probabilité dans ce cas :

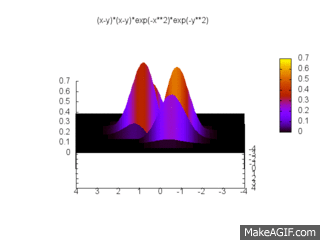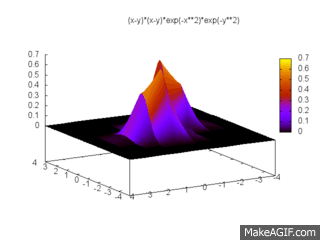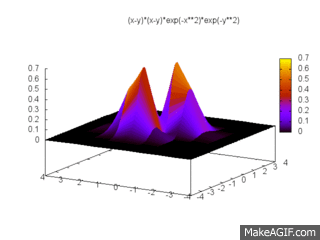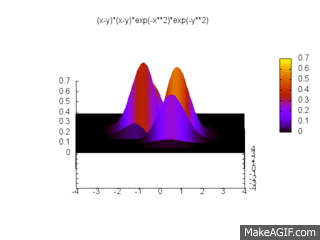
On la généralise pour N fermions indépendants de la manière suivante :

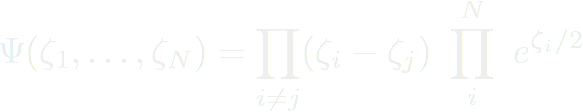
En ce qui concerne deux bosons sans interaction, la fonction d'onde s'exprime comme :

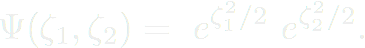
Ici, la symétrie bosonique est bien respectée. De la même manière, N bosons indépendants auront pour fonction d'onde :

▼ En savoir plus ▼

Comme mentionné précédemment, nous voulons étudier des bosons et des fermions sans interaction, et ce, en les piégeant dans un puits de potentiel harmonique.

Il nous faut résoudre l'équation aux valeurs propres suivante :

Afin d'en trouver les solutions analytiques et dans le soucis de rendre le calcul intelligible, nous résolvons dans un premier temps le problème pour une unique particule. L'hamiltionien s'écrit donc :

Et l'équation devient :

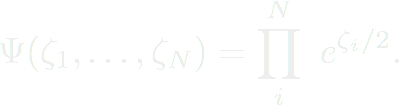
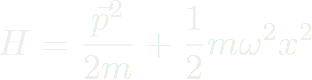
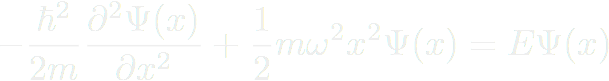
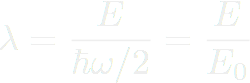
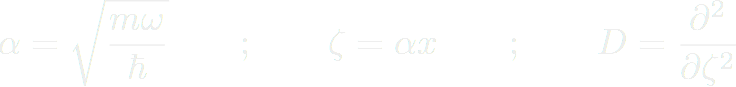
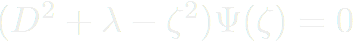
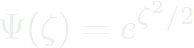
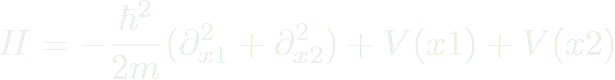
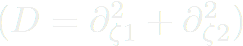Connaissant l'expression quantifiée des énergies dans un puits de potentiel harmonique formule fonction d'onde nous exprimerons les grandeurs en unité d'énergie :

Par ailleurs, on change également l'échelle de longueur :

Finalement l'équation se résume à l'expression :

La solution analytique de cette équation s'écrit :

Lorsque que l'on s'intéresse à deux particules, il s'agit de savoir si ce sont des bosons ou des fermions. En effet, l'un respecte une symétrique et l'autre une antisymétrie.

L'hamiltonien sans interaction s'écrit :

En exprimant la même équation aux valeurs propres et en effectuant les mêmes changements de variables formule fonction d'onde , on doit résoudre :

S'il s'agit de deux fermions la solution à cette équation s'écrit :

respectant l'antisymétrie de sa famille ainsi que le principe d'exclusion de Pauli. Soit dit en passant, on peut généraliser ce résultat pour N fermions dans un puits de potentiel ; la fonction d'onde prend pour expression :

Si à contrario, il s'agit de deux bosons, la solution à cette équation s'écrit :

respectant quant à elle, la symétrie de son genre. Elle se généralise à N corps telle que :

Ces fonctions d'ondes sont indispensables dans l'élaboration des méthodes numériques nous permettant de modéliser le système ; méthode que nous préciserons dans l'onglet "Metropolis".

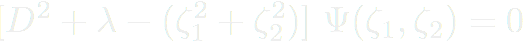
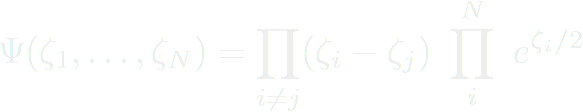
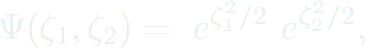
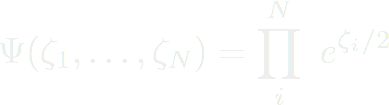
Nota Bene : Si on considère des bosons avec une interaction infinie, alors ceux-ci se comportent comme des fermions, à une phase près. On parle de fermionisation des bosons. Sa fonction d'onde est de la forme et respecte la symétrie bosonique.