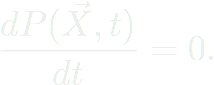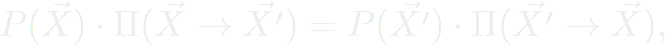Métropolis

La méthode de Monte-Carlo Metropolis est une méthode numérique basée sur l'utilisation de nombres aléatoires. Cet algorithme peut se décliner en plusieurs étapes :

1. On commence avec une certaine configuration des particules, de positions (x₁,x₂,...,x_n) ; ce sont les conditions initiales.
2. La probabilté correspondante s'écrit P(x₁,x₂,...,x_n).
3. On propose la variation d'une des variables, exemple : x₁ → x₁ + δ = x'₁.
4. On calcule la probabilité de cette nouvelle configuration, soit P(x'₁,x₂,...,x_n).
5. Si P(x'₁) > P(x₁), on accepte le changement de configuration.
6. Si P(x'₁)< P(x₁), on accepte le changement avec une probabilité de P(x'₁)/P(x₁).
7. On réitére l'opération.

Ce procédé va permettre aux particules de se rapprocher progressivement de leur état d'équilibre. Au fil des répétitions, les configurations acceptées épouseront de manière statistique les états les plus probables. En somme, plus le nombre d'itérations sera grand, plus la modélisation s'accordera statistiquement avec ce qu'il se passe réellement au sein du système. Cette "recette de cuisine" suit une équation qui décrit le système à l'équilibre, nommé "bilan détaillé".

▼ En savoir plus ▼

Le bilan détaillé reprend, pour se construire, la définition même d'un état d'équilibre : un ensemble est à l'équilibre si la probabilité de sa configuration ne fluctue pas en fonction du temps. Autrement dit :

Cette non-fluctuaction peut aussi s'exprimer de la manière suivante : à l'équilibre, le nombre moyen de déplacements acceptés à partir d'un quelconque état X vers n'importe quel état X' est exactement égal au nombre de déplacements inverses.

où π(i → j) est la probabilité de passer d'un état i à un état j. Les opérations algorithmiques mentionnées ci-dessus ont pour unique but de respecter progressivement le bilan détaillé et construisent de fait un système qui tend vers son état d'équilibre.