L’objectif de cette partie sera d’étudier le comportement d’un plus grand nombre de particules indiscernables (vingt particules typiquement). Elle tâchera notamment d’en examiner la répartition spatiale et d’analyser les densités.

En particulier, nous souhaitons principalement répondre à une question : dans un milieu libre, comment se répartissent des fermions et des bosons indépendants et quelle est la distribution des intervalles séparant deux particules ?

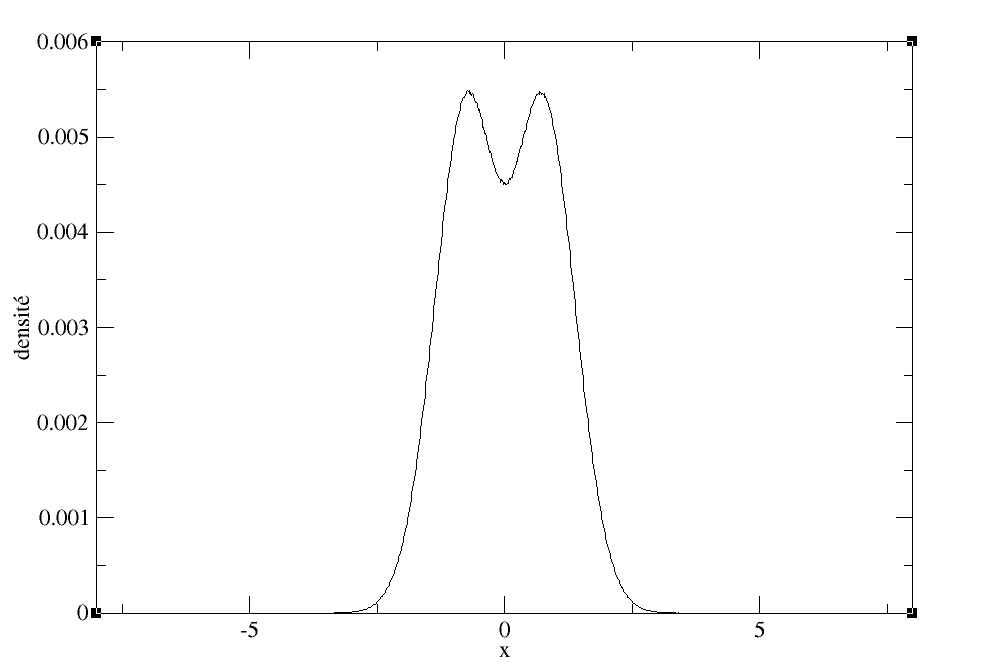
Débutons tout d’abord par extraire le profil de densité selon le nombre de fermions indépendants :

Lorsqu’il s’agit de deux fermions, le résultat n’est pas surprenant, on y retrouve la forme de la coupe transversale de la densité de probabilité correspondante.

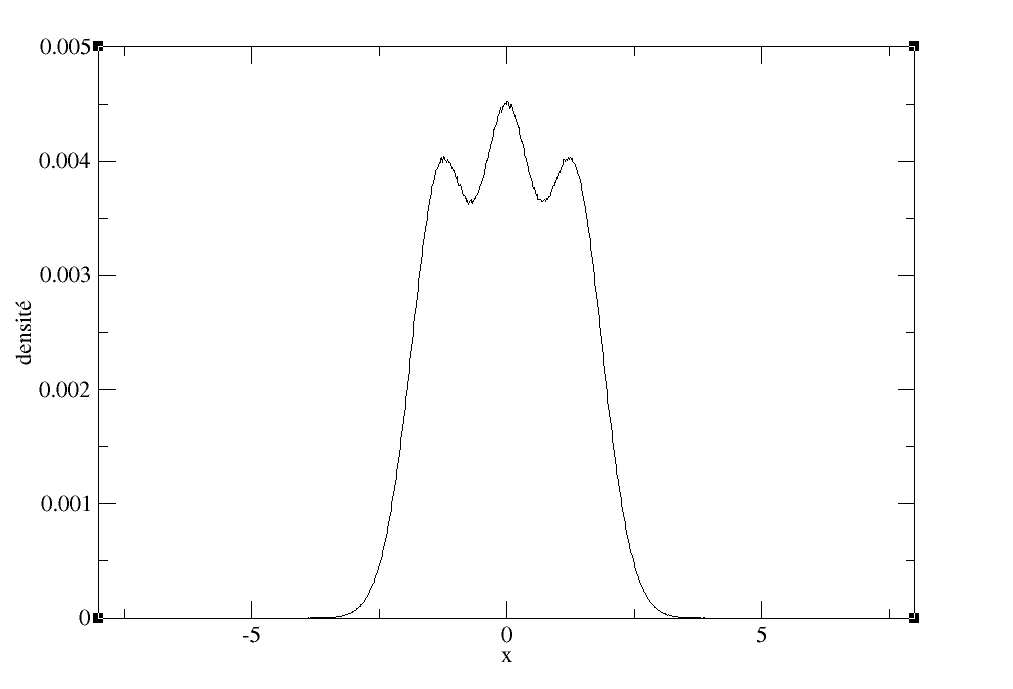
Au sein d’un puits de potentiel, la probabilité de trouver une particule en son centre est plus importante que celle d’en trouver une sur ses bords. C’est ainsi que la densité respecte ce principe ; plus on augmente le nombre de particules, plus on observe se dessiner en filigrane le profil du puits dans lequel elles sont piégées.

Dans ce projet, l’introduction d’un piège harmonique n’a qu’un seul but : déterminer une zone où toutes les particules se regroupent afin de mieux pouvoir les étudier. Cependant, la présence d’un tel paramètre dans l’étude de ces particules n’est pas systématique. Ainsi, nous cherchons des résultats plus généraux que ceux exposés dans ce cas précis. En effet, les particules étant plus « serrées » au centre du puits que sur ses bords, la répartition des particules en est conditionnée et n’a rien d’universel.

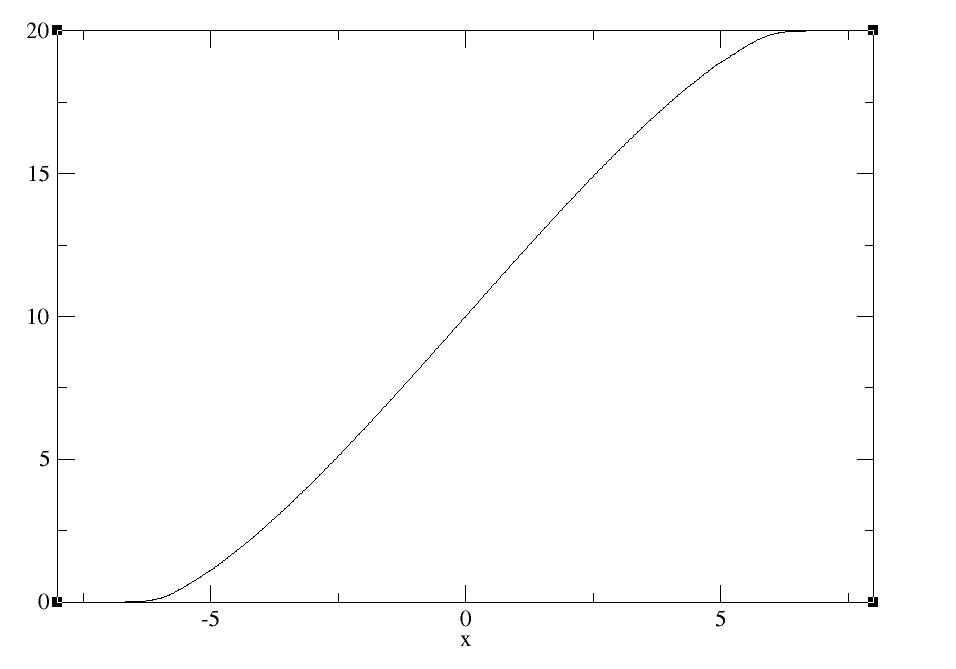
En partant de nos résultats, nous devons trouver un moyen de nous affranchir des effets du piège harmonique. À ce dessein, la fonction de comptage semble donner une solution. La fonction de comptage est une fonction qui « compte » le nombre de particules d’une borne inférieure fixe (en général -∞) à une borne supérieure mobile (x). En mathématiques, on la nomme fonction de répartition d’une distribution.

On peut brièvement commenter cette figure. On observe une forte pente de la courbe dans la zone centrale et au contraire, une pente plus faible sur les extrémités : le milieu du puits étant plus dense, c’est bien là que la fonction de comptage croît le plus rapidement.

Une question demeure : en quoi cette fonction de comptage va-t-elle aider à nous libérer du piège harmonique ?

Soit N(x) la fonction de comptage. On sait qu’à chaque tirage, une nouvelle configuration (x₁, x₂, …, x_N) est proposée. Puisqu’orientée par la présence du puits, nous devons recalculer chaque configuration afin d’uniformiser la densité, sans pour autant perdre l’information sur la répartition des particules indiscernables.

Pour ce faire, il suffit de remplacer chaque position d’une configuration par la fonction de comptage correspondante. Plus concrètement, la configuration (x₁, x₂, …, x_N) devient (N(x₁), N(x₂), …, N(x_N)).

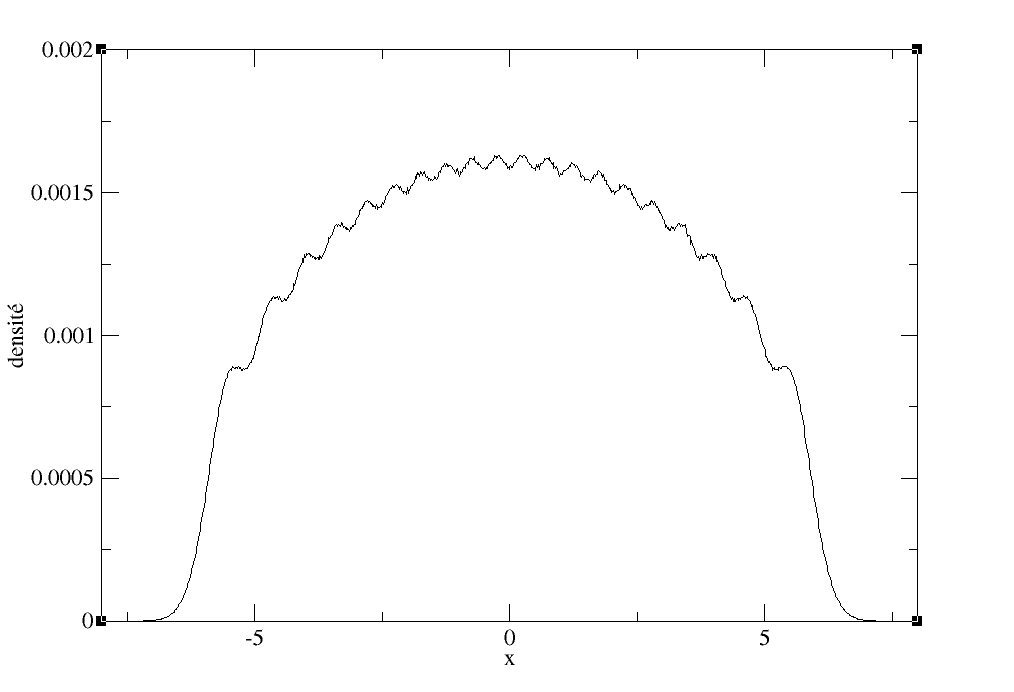
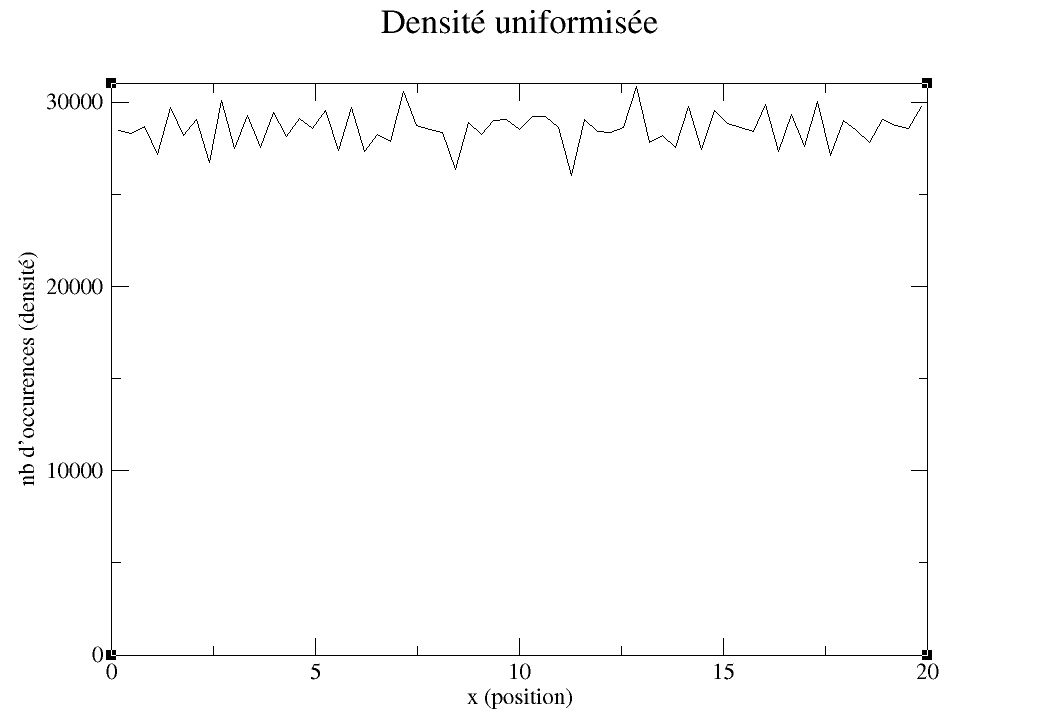
La visualisation de la nouvelle densité témoigne de son uniformisation, aux fluctuations statistiques près.

Cette étape terminée, nous pouvons à présent étudier la statistique des intervalles entre premiers voisins. Avant de les répertorier dans un tableau, nous devons tout d’abord trier par ordre croissant les configurations. En effet, les particules étant indiscernables, la variable x1 ne constitue pas la trajectoire d’une particule bien identifiée. Sa valeur est donc celle d’une particule dans le milieu, mais on ne peut pas en savoir plus. Si on se forçait à distinguer spatialement les particules (bien que cela ne soit pas correct), on pourrait dire que x1 peut concerner la particule 1 à l’étape 1, puis la particule 4 à l’étape 2.

En raison du grand nombre d’opérations déjà demandé à l’ordinateur, nous optons pour un « tri rapide » que nous insérons dans le programme.

Nous sommes désormais dans la capacité de collecter toutes les données des intervalles entre premiers voisins dans un tableau, puis d’en tracer la distribution.

Par soucis de précision, un grand nombre d’itérations est requis pour un résultat acceptable (typiquement 100 millions). Ceci implique d’exécuter le programme sur une longue durée, entre 45mn et 1h30 selon les ordinateurs.

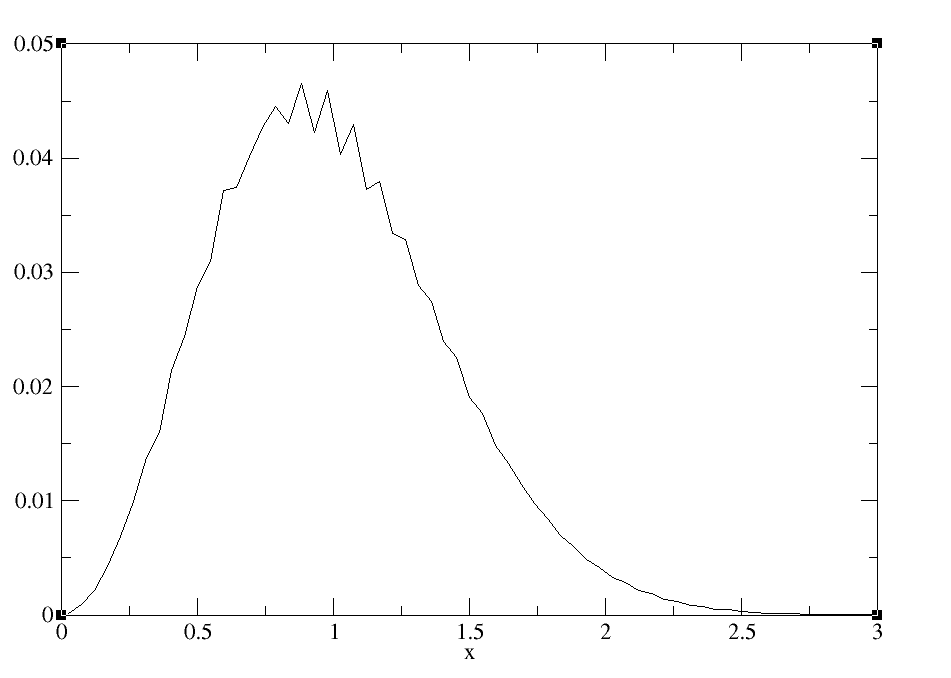
On obtient finalement la distribution des premiers voisins pour vingt fermions indépendants :

Commentons ce résultat. Il est important de dire que cette distribution décrit aussi bien des fermions indépendants (sans interaction) que des bosons avec une interaction infinie (voir fermionisation des bosons dans « Notre Rapport »).

Plusieurs points sont à noter :

• Premièrement, la distance avec le premier voisin n’est jamais nulle, on peut donc constater que ces particules se « repoussent » et ce, sans aucune interaction. Ce phénomène est simplement dû à la symétrie des particules concernées.
• Secondement, on observe que les fluctuations de cet intervalle sont de l’ordre de sa moyenne, ce qui s’apparenterait plutôt à un milieu liquide.
• Enfin, nous avons essayé d’analyser la loi de croissance et de décroissance de la figure. Il se trouve qu’elle ne correspond ni à une loi de puissance, ni à une loi exponentielle.

On peut aussi conjecturer sur les résultats que nous auraient donné vingt fermions indépendants en la présence du puits. On trouverait la même figure que dans un milieu libre, mais translatée vers 0 et compressée au fur est à mesure que l’on s’approche du centre du puits. Le centre du puits étant plus dense, on comprend que la distance entre les particules, tout comme ses fluctuations, sont plus faibles, mais elles garderaient les mêmes proportions que dans le cas étudié.

Bosons indépendants

Afin de comparer les résultats obtenus avec vingt fermions indépendants, il nous faut ici étudier le comportement de vingt bosons indépendants dans des conditions similaires. On pourrait très bien modifier le contenu du programme, changeant le calcul de la fonction d’onde des fermions pour celle des bosons, puis exécuter le même algorithme.

Néanmoins, il se trouve qu’une approche plus simple à mettre en œuvre donne le même résultat : le tirage successif des configurations pour les bosons sans interactions dans un milieu libre revient à effectuer un tirage selon une loi uniforme.

Ainsi, nous élaborons un autre programme qui tire vingt positions aléatoires de manière uniforme, proposant une configuration. Nous répétons l’opération un grand nombre de fois, puis, à l’instar des fermions indépendants, extradions les données dans le but de constituer une statistique de la distance au premier voisin.

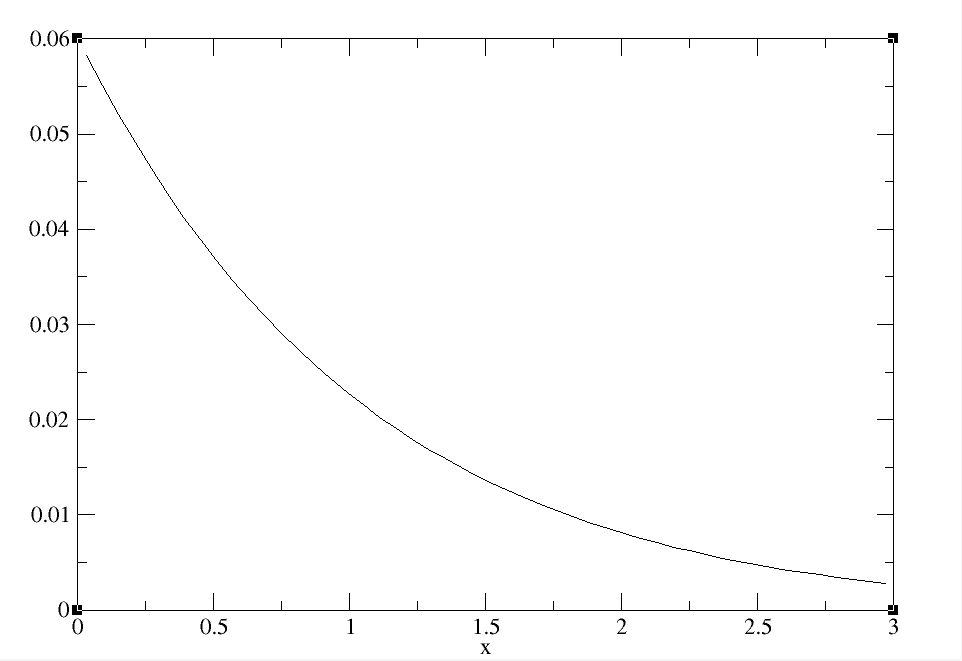
Sans étonnement, les résultats sont diamétralement différents de ceux des fermions. Les bosons sans interactions ne se « repoussent » pas, et au contraire, ils « s’attirent ». Du moins, la probabilité que l’intervalle entre deux bosons soit nul est plus importante que pour n’importe qu’elle autre proposition.

Si on analyse de plus près la loi de décroissance, elle suit une loi exponentielle ; en témoigne la même figure représentée en échelle semi-logarithmique :