• REGIME CHAOTIQUE

                 En étudiant ce système (figure ici), on observe que les îlots de résonance ne sont pas contenus par des formes elliptiques, mais ils se situent à l’extérieur de ces formes. On peut se demander si ces îlots sont toujours aussi stables qu'auparavant.

Si l’on trace la section de Poincaré d’un rayon dans une de ces résonances, on note qu’il y a toujours stabilité, le rayon est guidé à travers ces résonances. Par contre, si l’on change les conditions initiales, et qu’on injecte un rayon juste à côté d’une de ces résonances, le rayon suit une trajectoire complètement différente, et surtout instable. En effet, le rayon n’est plus guidé et il sort du guide d’onde.

On note la grande différence de stabilité entre ces deux cas. D’un côté des rayons qui sont émis dans une résonance et qui sont guidés sur des zones précises de chaque segment et ce jusqu’à l’infini. Tandis que pour une petite variation des conditions initiales, nous avons un rayon qui sort du guide d’onde.

Et pour les rayons qui sortent, le phénomène est aléatoire car le rayon peut sortir plus ou moins vite comme on peut le voir sur ces deux trajectoires :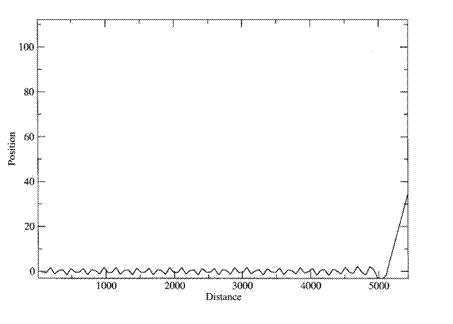

 Position 0, Angle -4°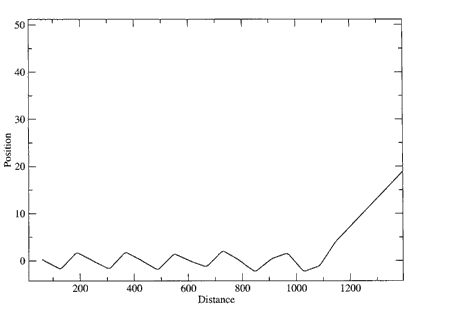

 Position 0.2, Angle 4°

Ce contraste de stabilité pour une variation minimale des conditions initiales est appelé « Chaos ». Ici nous sommes donc en présence d'un régime chaotique (ou système mixte, car il y a des zones de stabilités)entre les résonances dans lesquelles il y a guidage du rayon, et les points autours où celui-ci n'est plus guidé.

On peut aussi envoyer un rayon entre deux ellipses et voir ce qui s’y passe : (trait rouge)

Section de Poincaré de rayons entre deux ellipses 

Dans les sections de Poincaré on remarque que le rayon décrit encore une ellipse mais qui, cette fois-ci possède une certaine épaisseur. L'ellipse est décrite par un nuage de points.

Si l’on regarde la trajectoire on remarque le faisceau ne passe jamais vraiment par les mêmes points, même s'il est cantonné entre les deux ellipses, il décrit une trajectoire aléatoire entre ces deux ellipses.

Si l’on envoie un autre rayon, toujours entre ces deux ellipses, avec une différence au niveau des conditions initiales par rapport à celles du cas précédent (angle ou position d’entrée différents), sa trajectoire est, comme pour les deux rayons non guidés vus sur les figures ci-dessus, différente de celle obtenue précédemment.

Il paraît donc impossible de prévoir le trajet effectué par un rayon placé dans ces zones.  Ici, on  peut donc parler de  "chaos à petite échelle" c'est-à-dire que la trajectoire est aléatoire mais  est cependant entourée par les deux ellipses.