•         THEORIE

 
Nous établirons ici les équations régissant la propagation de rayons lumineux dans des guides d'ondes selon leur profil d'indice.

1 Modélisation d'un guide et grandeurs caractéristiques

● Fibre optique: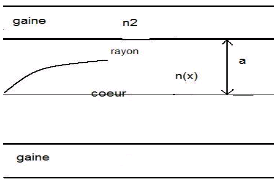

avec : a : le rayon du coeur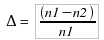
           n2 : indice de la gaine
on notera n1 = n(x=0)
et on posera :  

● Guide segmenté :

avec d : largeur d'un segment
        Λ : période de la segmentation

On définira également le rapport cyclique :

Pour les deux types de structure, on considérera que ox est l'axe vertical et oz l'axe horizontal (axe optique). L'origine du repère sera en z=0 et au centre du guide.

2 Equation générale du rayon

Tout d'abord, il s'agira de déterminer l'équation des rayons se propageant dans un guide d'onde dont le profil sera défini par n(x).

    Considérons qu'une variation continue d'indice peut être vue comme une variation discontinue sur des éléments différentiels dx afin d'appliquer la loi de Snell-Descartes de la manière suivante :

L' indice varie selon n(x).

La loi de Snell-Descartes s'écrit :

n1.cos(θ1) = n2.cos(θ2) = ... =f(θo)

Et on pose :  f(θo) = β

Pour une variation différentielle, on a :

dS² = dX² + dZ²
donc

et comme

alors :

Ainsi, on obtient l'équation différentielle suivante :

Que l'on dérive par rapport à z :

<=>
<=>
<=>

Ainsi, l'équation différentielle décrivant le rayon est :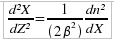

Nous étudierons par la suite deux cas de profil d'indice : le profil parabolique et le profil gaussien.

3 Guide au profil d'indice transverse parabolique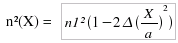

Pour un profil parabolique, l'indice s'écrit de la manière suivante :

3 1 Profil parabolique

Pour un guide  non segmenté, l'indice vaut : n (x) pour |x| < a

                                                                                              n2 pour |x| > a

Ainsi, pour |x| < a ,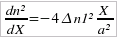

et si on pose :

l'équation du rayon devient :

<=> 

Dont la solution est de la même forme que pour un oscillateur harmonique :

x(z) = Asin (Γz) + Bcos(Γz)

Déterminons les constantes A et B :

● Si on injecte un rayon au centre du guide d'ondes, alors x(z=0) = 0.

Ainsi, B = 0 et il ne reste que : x(z) = Asin(Γz)

● On sait qu'à “l'entrée” du guide, on a :

 donc  

Ainsi, pour un profil d'indice parabolique, l'équation du rayon dans la fibre est :

Nous pouvons déduire de cette équation que les trajectoires du rayon dans le guide à profil d’indice parabolique sont des sinusoïdes dont la période d'oscillation T vaut :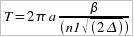 

3 1 Profil gaussien

Pour un profil gaussien, l'indice s'écrit de la manière suivante :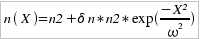

               

donc

et   car  

et

Ainsi, pour |x| < a , l'équation du rayon est définie par :

Il n'existe pas de solutions analytiques à cette équation et nous sommes donc contraints d'avoir recours à des solutions numériques.