La tomographie sismique
exemple pour la couche 2:
Donc pour les vitesses on a juste à prendre l'inverse des coefficients directeurs.
détermination des hauteurs :
Il faut déterminer l'ordonnée à l'origine. Puis calculer les angles d'incidences
(il faut recalculer tout les angles à chaque couche)
Pour calculer cet angle nous utilisons la formule de Snell-Descartes aux limites c'est à
dire quand l'onde incidente arrive avec un angle correspondant à l'angle limite,
l'onde réfractée se propage à 90° (elle reste à l'interface de 2 strates et
et se propage à la vitesse caractérisant la couche inférieure)
Exemple couche 3 :
Snell-Descartes
Une fois tout les angles déterminés, ainsi que l‘ordonnée à l'origine. On pose
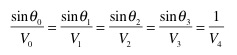
Ici c'est l'onde réfractée à la limite couche 3 / couche 4 qui est refractée avec un angle de 90° donc le sinus de l'angle vaut 1.
Une fois que l'on a tout les angles, on pose enfin:
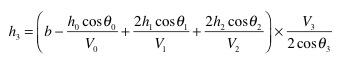
Voilà la méthode utilisée pour déterminer les différentes vitesses et hauteurs de couches.
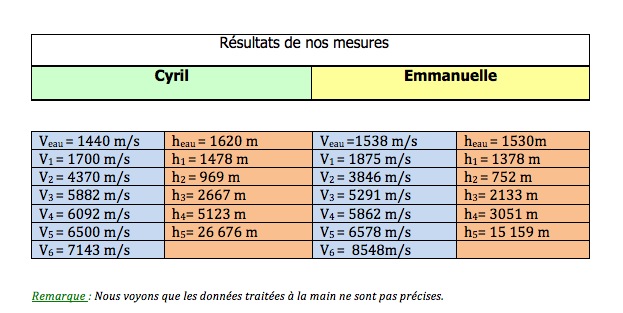
On récupère ainsi un premier modèle du sous-sol : le nombre de couches, leurs profondeurs
ainsi que leurs vitesses caractéristiques.
Nous avons tout les deux trouvé qu'il y a 6 couches mais nos valeurs des profondeurs et vitesses de propagation
sont relativement différentes, témoignage des limites de cette méthode d'exploitation qui reste très approximative.
Dans la plus part des cas on ne peut pas utiliser cette méthode dont les hypothèses initiales
simplifient de manière abusive la constitution du sous-sol. Il faut donc faire appel à des méthodes
tomographiques fondées sur le calcul de temps de trajet dans des milieux d'hétérogénéité quelconque
(problème direct) et sur la résolution d'un problème d'optimisation (problème inverse).