• Accueil
• Principe de la sismique
  • Notion trajet d'onde
• Méthodes d'acquisitions
  • Sismique réfléxion
  • Sismique réfraction
  • Exploitation d'un sismogramme
• Méthodes d'exploitations
  • Le problème inverse
  • Exploitation manuelle
  • Exploitation numérique

Théorie du problème inverse:

Le problème inverse est un principe d'optimisation permettant de retrouver les propriétés du sous-sol. Il est ainsi nommé car le principe est de reconstruire un modèle du milieu à partir de données physiques. Par opposition au problème directe qui consiste dans le cadre de la tomographie des temps de trajets à calculer les temps de trajets d'ondes se propageant dans des milieux connus.

Nous allons pour cela considérer une relation non linéaire entre les données d, (ici ce sont les temps que nous avons récoltés) et le modèle (du sous sol que nous cherchons à construire) m :

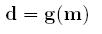
g est un opérateur et la relation est non linéaire. Nous allons donc chercher à la linéariser: on établit une estimation de m
et de d:

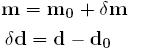
avec : 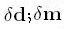perturbation des données et du modèle.

On les remplace dans l'équation afin d'obtenir un modèle de perturbation:



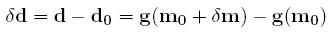
On effectue un developpement de Taylor au premier ordre afin d'obtenir une relation linéaire:



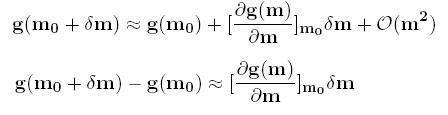
On modifie le modèle de perturbation et on obtient:


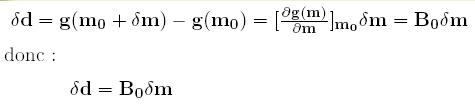
relation linéaire avec Bo dérivée de Fréchet.