Pour voir si l'on peut retrouver des similitudes entre les comportements géométrique et ondulatoire, il a fallu faire des simulations de propagation dans notre fibre.
Pour cela, nous avions à notre disposition un programme déjà écrit faisant intervenir un méthode de calcul bien précise : la BPM (Beam Propagation Method), programme que nous avons adapté à la géométrie de notre fibre.
Principe de la BPM :
"La méthode du faisceau propagé repose sur l'idée qu'une onde optique dans un guide
d'onde est soumise à deux phénomènes. D'une part, la structure dans laquelle l'onde se propage
est guidante. Nous avons vu dans l'approximation de l'optique géométrique que l'on
pouvait assimiler le guidage de l'onde à la réflexion de rayons sur les contours du guide.
D'autre part, la nature ondulatoire de la lumière induit un phénomène de diffraction.
Le principe de la BPM est le suivant: la distance de propagation est discrétisée avec un pas
z suffisamment petit, et il est alors possible de traiter séparément la propagation guidée et la diffraction, sur chaque pas.
Une vision schématique du guide d'onde est alors une succession de lentilles convergentes
qui modélisent le confinement de la lumière, séparées par un espace de propagation libre qui
est associé à la diffraction."
[Claire MICHEL, Thèse de doctorat Chaos Ondulatoire en Optique Guidée : Amplificateur fibré double-gaine pour la génération de modes "scar", chapitre 4 : amplifications de scars "numériques", Nice, 2009.]
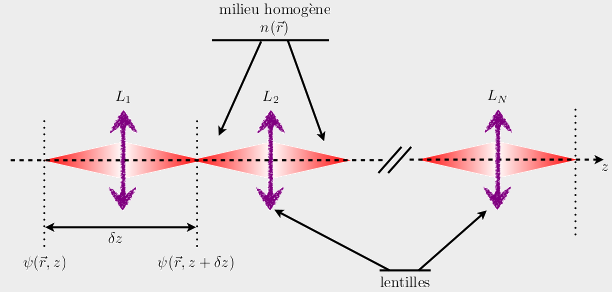
FIGURE 9 : Schématisation d'un guide d'onde
Fonctionnement du programme :
Une partie des paramètres du système sont à fixer lors de l'éxécution du programme :
• longueur de la fibre
• pas de stockage de l'intensité du champ
• choix de la géométrie (circulaire ou tronquée, où la troncature est fixée dans le code)
• choix de l'excitation (onde plane ou faisceau gaussien)
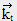. A partir de là, le programme simule la propagation sur la distance souhaitée en enregistrant le champ à chaque pas de stockage, permettant ainsi de visualiser son évolution au cours de la propagation.
Recouvrement et Spectre
Le recouvrement entre l'excitation et les modes de propagation est défini comme suit :
 |
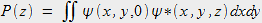(1) |
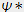est le complexe conjugué de 
.
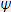En se reportant à l'équation (1) de la page précédente, il vient :
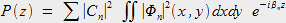
Mais chaque fonction
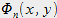étant normalisée on a :
 |
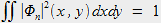(2) |
On en déduit alors l'expression finale pour le recouvrement :
 |
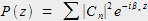(3) |
Pour avoir le spectre, il faut une fonction dépendant de
, on calcule donc la transformée de Fourier
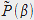du recouvrement et l'on obtient alors :
 |
 |
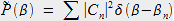