Un peu de théorie ...



Equation de propagation :

Comme toute onde propagative, la lumière obéit à l'équation de propagation (tirée des équations de Maxwell-Faraday et Maxwell-Ampère).

Soit une onde monochromatique de forme générale :

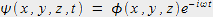
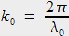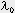où , et longueur d'onde dans le vide.

L'équation de propagation s'écrit alors :

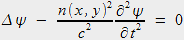
où n(x,y) vaut so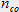it soit 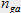selon où l'on se trouve dans la fibre.

[Valérie DOYA, Thèse de doctorat : Du Speckle aux Scars, une expérience de chaos ondulatoire dans une fibre optique, Nice, 2000.]



Les modes de propagation :

Toute onde qui se propage dans la fibre peut se décomposer sur la base des modes propres de propagation,notés
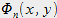
On écrit alors :
(1)


Où les coefficients 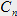sont a priori complexes. Ils correspondent au poids de chaque mode induit par la condition initiale.

On distingue deux types de modes :

• Les modes réguliers : Ce sont les modes observés lorsque l'on envoie l'onde le long d'une orbite périodique, qui gardent la géométrie du système.
• Les modes irreguliers : Il s'agit de tous les autres modes sans signature particulière.


Il est également intéressant de calculer la transformée de Fourier de la fonction d'onde par rapport aux variables x et y. En effet, cette opération mathématique s'écrit comme suit :

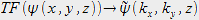
Mais 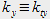et 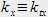. Autrement dit, le calcul de la transformée de Fourier permet d'obtenir une représentation des coordonnées du vecteur d'onde transverse et d'avoir accès à sa répartition angulaire dans l'espace des fréquences spatiales. Cette représentation est un outil permettant de caractériser la régularité des modes: c'est la méthode du champ lointain - qui apporte un complément à l'observation du champ proche, i.e, l'observation de l'intensité du champ - présentant l'avantage d'être accessible à la fois numériquement et expérimentalement.



Comment retrouver des modes réguliers dans la fibre?


Si les modes ne peuvent être connus qu'en les calculant mathématiquement - cela ne se faisant que numériquement - et le but de nore projet n'étant pas là, on peut néanmoins les identifier qualitativement. Pour cela, on envoie une onde plane de la form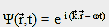e le long d'une orbite périodique de longueur L. Pour pouvoir observer les modes - ici des modes réguliers -, il faut donc nécessairement que les ondes incidente et réfléchie soient en phase, ce qui donne lieu à une condition d'interférences constructives, à savoir que le déphasage 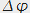entre les deux ondes doit être un multiple entier de 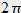, soit:



A cela s'ajoute le déphasage 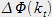lié à la réflexion sur les bords de la fibre :
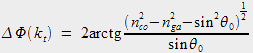(2)

Quant au déphasage total, il peut être déduit de l'onde plane dans le plan transverse :

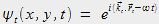
où 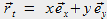est le vecteur position transverse.

Il apparaît alors clairement que le déphasage total correspond à la partie spatiale de l'exponentielle complexe :

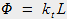
Avec L la longueur de l'orbite.
On obtient alors :

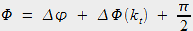
Le terme additif en 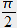est dû à la refocalisation de la lumière.
On a dès lors :


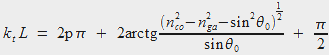
Et en considérant n rebonds -donc n réflexions- sur le contour, on a :
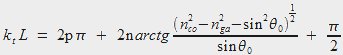(3)

Enfin, en se référant à la figure 7, on obtient :


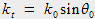
En injectant cette relation dans l'équation (3) on a finalement :
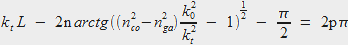(4)


C'est une équation transcendante dont on peut trouver les solutions numériquement. Remarquons aussi que cette équation impose la quantification de la norme de 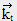et par conséquent celle de 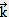pour des modes réguliers le long d'orbites périodiques.