Approche Géométrique - Matrice de transfert
Comme dit précédemment, on peut caractériser la stabilité de cette orbite périodique à l' aide des matrices de transfert.
On note (s0,p0) le couple «abscisse curviligne-angle» servant a repérer la condition initiale dans l’ espace des phases. En partant d'un point écarté d’ une distance ( s0 + δs0, p0 + δp0 ), où δs0 et δp0 sont petits devant s0 et p0,on peut écrire, qu’après N réflexions, les variations (δsN, δpN) évoluent comme :
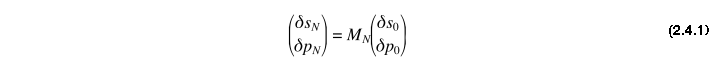
Où Mn est la matrice de transfert après N réflexions sur les bords du billard. On assimilera les bords de la fibre optique à des miroirs réfléchissants, faisant de celle-ci une cavité optique.
Afin d’avoir la matrice de transfert, le formalisme de l’ optique matricielle donne les matrices de réflexions notées R et de propagation notée P.

On cherchera alors en partant d’ un point donné, la matrice de transfert associée au trajet de l’ orbite périodique triangle, c’est à dire le chemin que prend le rayon pour retourner à sa position initiale. Ainsi on schématisera le chaînage de matrices nécessaire, en notant que les réflexions sur les parois incurvées se font suivant l' angle θ, déjà défini. De plus la paroi tronquée possède un rayon de courbure infini. La matrice de transfert associée à la réflexion du rayon lumineux sur cette paroi revient à l’ opposé de la matrice identité 2x2.
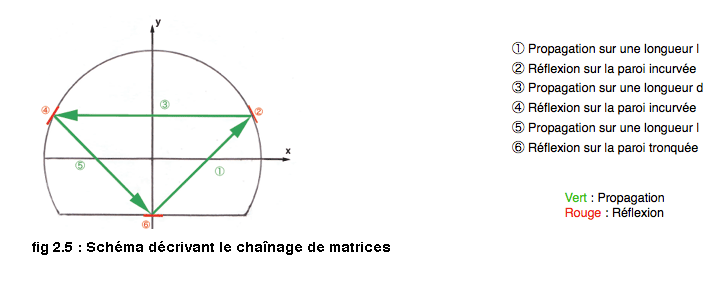
On obtient alors pour un rayon unité (calcul en annexe):
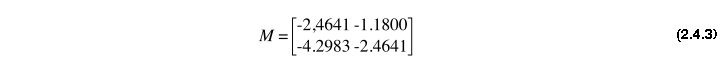
On peut à partir de là, étudier la stabilité de l' orbite périodique. On sait que :
![]()
Or les λ régissent la dynamique autour de l' OP3. Mais puisque ∣ Tr Mn ∣ > 2 les valeurs de λ sont réelles, il existe alors dans la dynamique qui régit l' évolution des écarts à l' orbite périodique, un terme exponentiel croissant qui tend à faire diverger le rayon hors de l' OP3. C'est donc une dynamique instable qui tend à faire croître les erreurs et fait ressortir les rayons hors de la trajectoire périodique.


