Approche Géométrique - Espace des phases
On sait déjà que le billard est un système fermé à 2 dimensions, répondant à des lois déterministes. C’est à dire que l’évolution d’un rayon est décrite par une succession de trajectoires rectilignes et de réflexions répondant aux lois de Snell-Descartes, dès lors qu'on posséde la connaissance du point d’ impact de la trajectoire sur le contour du billard, ainsi que l’ angle de réflexion on détermine parfaitement l’angle de réflexion suivant. La dynamique de la trajectoire se ramène alors à l’ évolution d’ une séquence de réflexions.
La trajectoire suivie par le rayon peut être représentée dans un espace appelé espace des phases.
Ce dernier peut être réduit à sa section de Poincaré, dont la représentation la plus courante se fait dans les variables (s , sin(θ)) où s est l’ abscisse curviligne qui est définie comme la position du point d' impact le long du contour de la fibre optique et θ l’ angle de réflexion par rapport à la normale au contour.
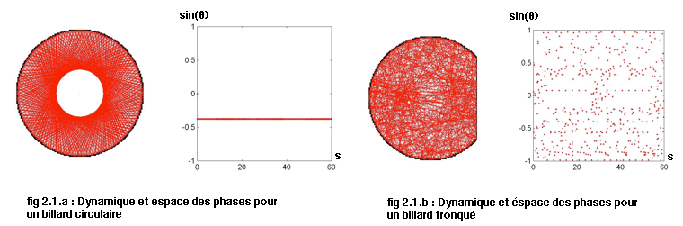
La dynamique des rayons dans les billards chaotiques est très différente de celle des billards réguliers. La dynamique régulière est illustrée dans la figure 2.1.a montrant une trajectoire typique dans le billard en forme de cercle tronqué et sa section de Poincaré tandis que dans la figure 2.1.b on observe la dynamique dans une fibre optique tronquée.
Pour un très grand nombre de réflexions dans la fibre optique tronquée , l’ espace des phases associé est entièrement et uniformément rempli.