approche Géométrique - L'OP3 en détail
Seul un triangle isocèle permet de re-boucler la trajectoire. Cette condition est imposée par la symétrie suivant l’ axe des abscisses. L’unique manière de construire ce triangle isocèle est de faire passer les rayons par le centre de la troncature. En effet, si cette condition n’ est pas remplie, les segments diagonaux ne seraient pas égaux et la trajectoire ne pourrait pas être périodique.
A cela, il faut rajouter qu’il existe un segment parallèle à la troncature.
Or les lois de Snell-Descartes imposent que l’ angle réfléchi soit égal à l’ angle incident.
Dés lors qu’on impose ces contraintes sur les angles, il apparait 2 points de chaque part des abscisses sur le triangle. Ces deux points appartiennent au cercle centré à l’ origine et de rayon R et de plus ils appartiennent à l’ une ou l’ autre des trajectoires diagonales de l’ OP3. Afin de déterminer les cordonnées de ce point, on se focalisera sur le point M des abscisses positives et on cherchera à déterminer ses coordonnées pour un rayon unité:

Une fois toutes les conditions sur les angles et longueurs prises en compte, on peut fixer l'angle et les longueurs caractéristiques à la seule valeur du rayon de la fibre optique (détail du calcul en annexe) :
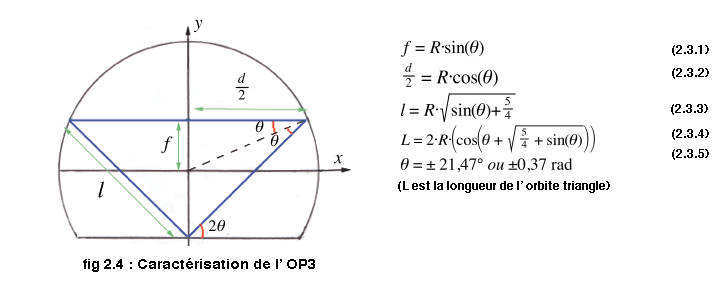
Maintenant que l' on possède toutes les données nécessaires, il est possible de caractériser la dynamique des rayons autour de cette orbite périodique.


