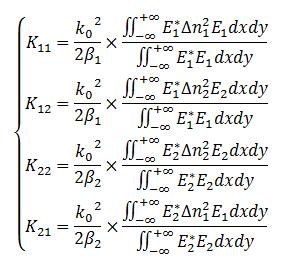LE COUPLEUR DIRECTIONNEL
Equations différentielles couplées
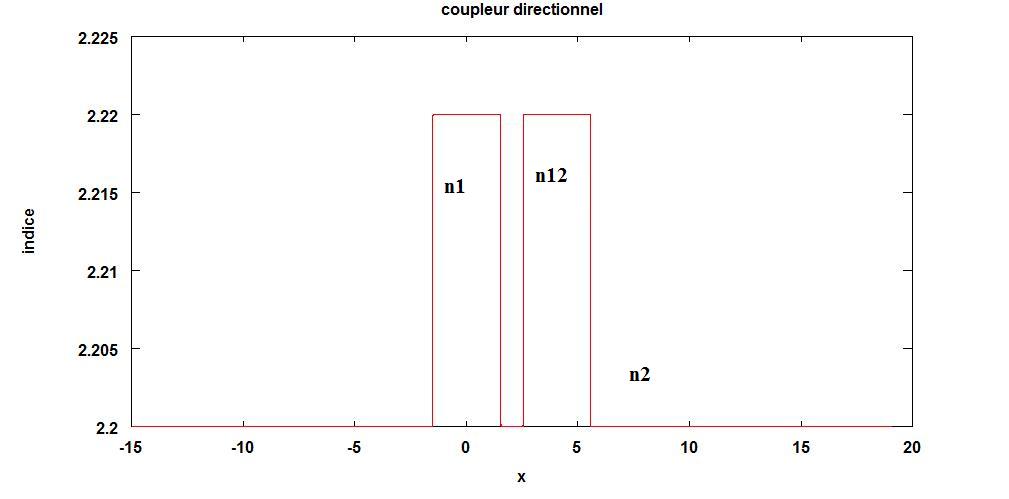
On considère deux guides diélectriques plans parallèles, d’indice de cœur n1 et n12 ; leurs cœurs ont une épaisseur d et sont séparés de w. L’indice de réfraction n2 qui les entoure est plus faible que les cœurs.
Photo d’un coupleur directionnel
Chaque guide d’onde en l’absence de l’autre est considéré monomode.
Lorsque le recouvrement
des deux profils est faible, on peut utiliser une théorie des
modes couplés.
Dans cette théorie
approchée, les modes dans chaque guide sont supposés
inchangés, soit pour le premier guide 
,
pour le deuxième 
,
et l’effet du couplage entre les guides est la modification de
leurs amplitudes A(z) et B(z) le long de la propagation.
A partir des équations
de Maxwell, on trouve que les équations couplées pour
les guides 1 et 2, en l’absence de l’autre, sont de la
forme :
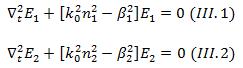
On pose E(x,y,z) comme
le champ total du coupleur directionnel, donc la forme des équations
devient:
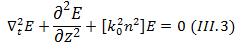
Où la constante
diélectrique
est représentée par le graphe suivant :
Et, en considérant les guides faiblement couplés, le champ total E est définit comme la superposition des deux champs.
En substituant la
définition de E dans (III_3), on néglige les termes
d’ordre 2 de l’équation différentielle car
les amplitudes varient lentement en fonctions de z.
Ensuite, à
l’aide des équations (III_1) et (III_2) on obtient
l’équation différentielle suivante :
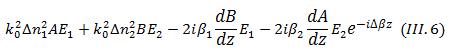
Où :
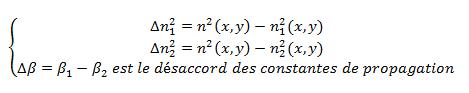
Ainsi en multipliant l’équation (III_6) par E1* et en intégrant, on obtient les deux équations différentielles couplées que suivent A(z) et B(z):
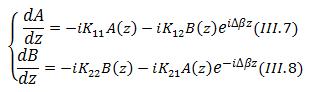
Où K11, K12, K22, K21 sont les coefficients de couplage réels et positifs égaux à :
