LE COUPLEUR DIRECTIONNEL
Equations des modes
Ici, nous choisissons la famille de mode TE (transverse électrique), ce qui nous permet de dire que le champ électrique est suivant l'axe y et que le champ magnétique est suivant l'axe x et z.
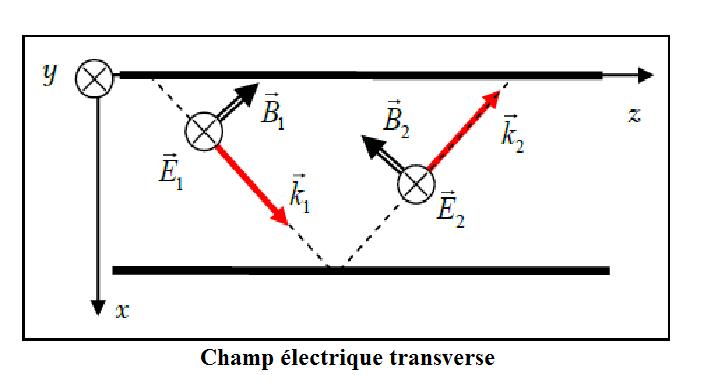
On peut donc simplifier les équations de Maxwell de la manière suivante:
 |
 |
 |
 |
 |
 |
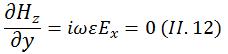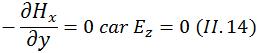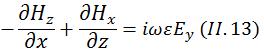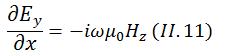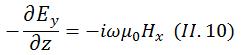Et, en remplaçant les équations (II_10) et (II_11) dans (II_13), on obtient l'équation suivante:
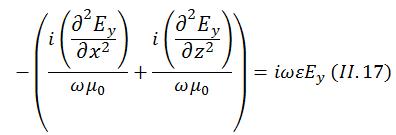
Or,
le champ électrique se propage dans la direction z et
l'intensité ne change pas, on écrit donc le champ
électrique sous la forme :
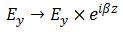où
l'exponentielle représente la constante de propagation.
On définit également les différentes variables:
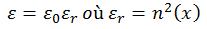
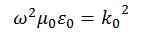
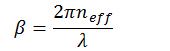
Où neff représente l'indice effectif que voit l'onde en se propageant dans le guide qui est compris entre la valeur de l'indice du guide et celle du substrat. Et β est la constante de propagation.
En
substituant ces variables dans l’équation (II_17), on
obtient :
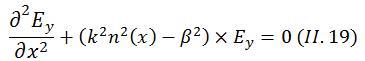
A présent cette équation ce décompose en deux cas : le premier est pour n(x)=n1 et le deuxième pour n(x)=n2.
Pour simplifier l’écriture, on pose deux constantes (premier cas) et (deuxième cas) :
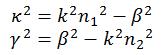
Pour le premier cas, on a une solution complexe qui représente l’onde qui se propage à l’intérieur du guide de la forme :
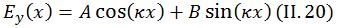
Pour le deuxième cas, on a des solutions réelles qui représentent la décroissance de l’onde à l’extérieur du guide :
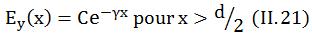
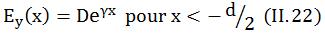
La
géométrie du guide et la continuité du champ
électrique font que :
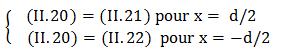
On
pose également B=0 car les solutions sont soit des sinus soit
des cosinus, cela nous permet de trouver les valeurs des constantes C
et D sachant que l’on a fixé A=1 pour la normalisation.
Ainsi,
on trouve les équations des modes suivantes :
