LE COUPLEUR DIRECTIONNEL
Puissance des Guides
Ici, on résout les équations différentielles couplées pour obtenir la valeur de la puissance transférée.
On utilise les
équations (III_7) et (III_ 8) où l’on
néglige, pour l’analyse théorique, les quantités
K11 et K22 qui représentent les corrections de la constante de
propagation de chaque guide d’onde due à la présence
de l’autre.
Ainsi, en dérivant
(III_7) par rapport à z, on élimine les termes
dépendant de B :
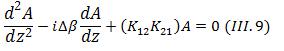
Donc, les solutions
générales sont de la forme suivante :
![]()
Où :
![]()
![]()
On déduit à partir de (III_7) et (III_10) la solution pour B(z) :
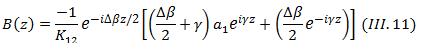
Pour calculer les valeurs des constantes d’intégrations a1 et a2, on fixe les conditions initilaes suivantes :
-l’amplitude lumineuse entrante dans le guide 1 est A(0)=A0
-l’amplitude dans le guide 2 est nulle, B(0)=0.
Finalement, on sait que la puissance est le carré de l’amplitude de l’onde, donc les puissances de chaque mode sont :
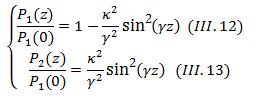
Où P1(0) est la puissance entrant dans le guide 1 à z=0.
La détermination de l’échange de cette puissance lumineuse entre les deux guides permet de lier les coefficients de couplage K12 et K21.