LE COUPLEUR DIRECTIONNEL
Page d'accueilLa constante de propagation
Les équations écrites précédemment donnent la propagation des modes dans le guide d’onde mais il faut encore déterminer la valeur de la constante de propagation pour que les équations soient complètes.
On détermine cette constante à partir de l’équation de dispersion.
Cette
équation est écrite à l’aide des dérivées
par rapport à x des équations (II-20) et (II_21) en
x=d/2, ainsi on obtient :
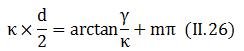
On
constate notamment que la constante de propagation ne peut prendre
que des valeurs discrètes parce que m est un entier, où
une valeur de m correspond à une seule valeur effective de
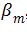 , donc un
seul mode TE.
, donc un
seul mode TE.
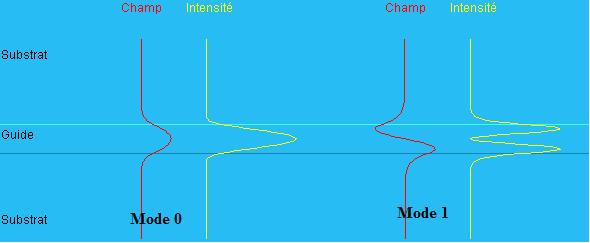
Modes dans un guide d’onde
L’onde
se propage dans le guide sous forme de mode comme représenté
sur cette image où les modes 0,1 sont représentés
en rouge.
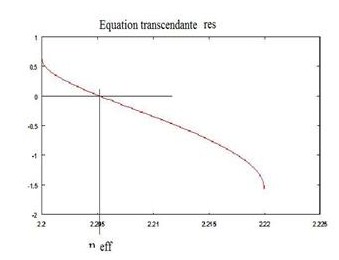
Pour résoudre cette équation, on utilise la méthode de dichotomie.
Et avec une résolution numérique de cette équation pour
le mode fondamentale (m=0), on obtient la valeur de l’indice
effectif ce qui permet d’en déduire les deux constantes
γ et κ :
La
connaissance de nos deux constantes, nous permet d’obtenir le
profil des modes.