Modèle des liaisons fortes
L'approximation des liaisons fortes consiste à regarder un solide comme un ensemble d’atomes neutres interagissant les uns avec les autres. En physique du solide, cette méthode permet de décrire les bandes d'énergies apparaissant dans un métal. Les électrons se trouvent dans des orbitales atomiques localisées autour de chacun des sites, l'interaction se fait par recouvrement des orbitales atomiques. Dans le cadre de notre système analogue, l'énergie de site correspond à la fréquence de résonance \( \nu_0 \), et le paramètre de saut correspond au terme de couplage, par ondes évanescentes, \(t\).
Système à deux sites
Dans l'espace direct, pour un système simple comprenant deux sites, le Hamiltonien de liaisons fortes s'écrit sous la forme suivante: \[\mathcal{H} = \left( \begin{array}{cc} \nu_0 & -t \\ -t & \nu_0 \end{array} \right) \] On rappelle que le couplage \( t \) est directement lié à la distance \(d\) entre les résonateurs. Afin d'alimenter ce modèle, la relation \(t(d)\) obtenue dans le rapport est ici utilisée.
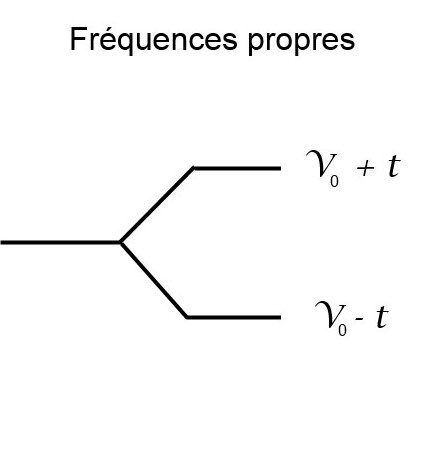
Note Usuellement, le couplage \(t\) est considéré positif. La fonction d'onde symétrique (resp. anti-symétrique) est alors associée au niveau d'énergie le plus bas (resp. haut). Dans notre système microonde, le couplage s'effectue via le champ magnétique, ce qui implique \(t < 0 \). La symétrie est donc inversée: la fonction d'onde symétrique (resp. anti-symétrique) est associée à la fréquence la plus haute (resp. basse) [4].
Evolution temporelle du système
Dans un cas plus général à \(N\) sites, pour un Hamiltonien qui ne dépend pas du temps, l'évolution temporelle de la fonction d'onde du système \(\Phi\) est régit par l'équation suivante: \[ i \hbar \frac{\partial}{\partial \tau} |\Phi \rangle = \mathcal{H} | \Phi \rangle \] La solution correspond à une combinaison linéaire des états propres \(\phi_n\) \[|\Phi \rangle = \sum_{n} c_n(\tau) |\phi_n \rangle \] avec \( c_n(\tau) = a_n e^{- i \nu_n \tau / \hbar} \), les coefficients \(a_n\) définissant l'état initial.
Simulations numériques
On se propose numériquement de diagonaliser le Hamiltonien \(\mathcal{H}\), d'en extraire états et valeurs propres (\(\phi_n\), \(\nu_n\)). Puis, à partir d'un état initial (\(a_n\)), de simuler son évolution temporelle.
A titre d'illustration, nous commençons par un système simple à deux sites. L'animation ci-dessous représente les évolutions temporelles de la partie réelle des modes propres correspondant aux féquences propres symétrique et anti-symétrique.