Capteur d'indice de réfraction
Capteur d'indice de réfraction final
Dans cette partie nous réalisons l'expérience finale, nous avons nos différentes solutions à base d'eau mélangées à du sel dont nous connaissons approximativement l'indice de réfraction. Nous allons donc effectué une série de mesure pour chaque solution et donc chaque indice de réfraction. Nous allons tout d'abord mesurer le spectre en remplissant le bac avec de l'eau, puis nous mesurerons le spectre pour chaque solution en gardant comme référence la courbe obtenue pour l'eau.
Le montage
Nous disposons toujours d'une fibre multimode (la fibre FTest) qui est soudée à chacune de ses extrémités à une fibre monomode (SMF 28). Celles-ci étant reliées à la source de lumière blanche pour l'une et à l'analyseur de spectre optique pour l'autre. La longueur de la fibre multimode utlisée ici est (62 ± 1) mm. La fibre multimode est placée sur le support qui est la plaque en métal, et le tout est placé dans le boîte rectangulaire qui est remplie avec le liquide souhaité (voir figure 1 et 2 ci-dessous).

Figure 1 : Schéma du montage SMS (SMF-MMF-SMF)

Figure 2 : Image de notre capteur d'indice de réfraction
Résultats
Nous avons effectué une mesure pour 8 indices de réfraction différents, nous présenterons ici les spectres obtenus pour 4 indices de réfraction :
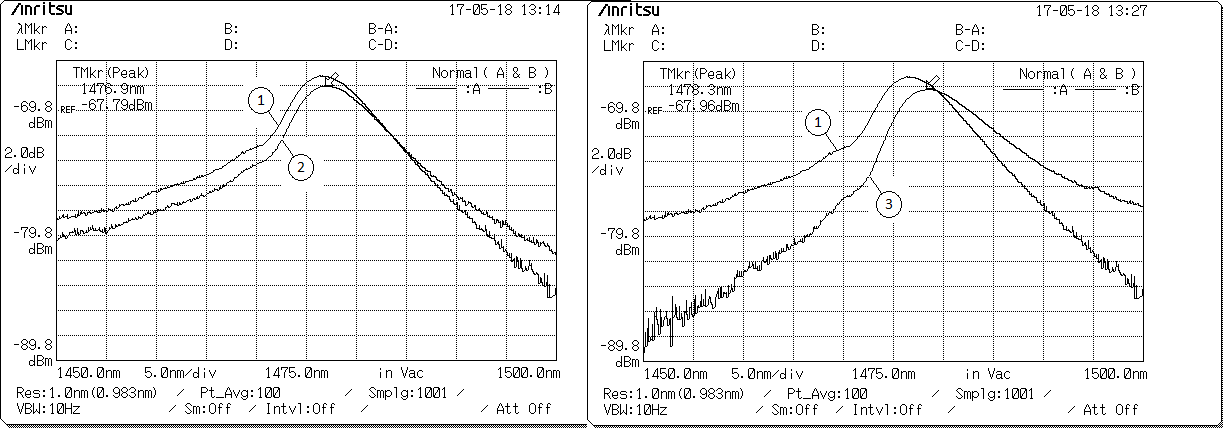
Figure 3 : Spectre de l'intensité (dB) en fonction de la longueur d'onde (nm) n=1,33 (1) n=1,33758 (2) n=1,34474 (3)
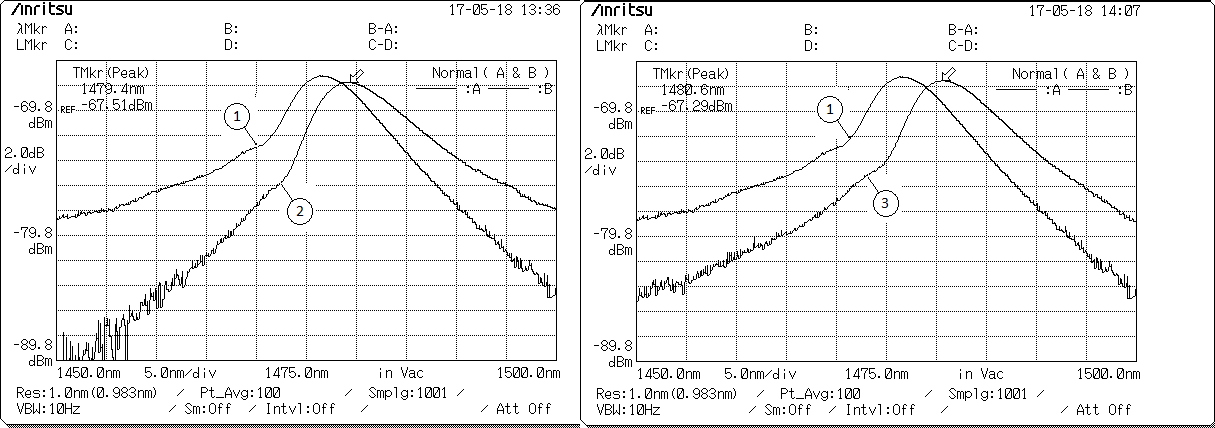
Figure 4 : Spectre de l'intensité (dB) en fonction de la longueur d'onde (nm) n=1,33 (1) n=1,3519 (2) n=1,37875 (3)
Comme nous l'attendions les pics se décalent vers la droite lorsqu'on augmente l'indice de réfraction. La sensibilité de notre capteur n'est pas extrêmement précise mais nous avons tout de même des résultats intéressants ; avec plus de travail la fabrication d'un capteur de ce type beaucoup plus précis et optimal doit être possible. Un de nos problèmes est que nous ne sommes absolument pas certain de l'indice de réfraction de nos solutions réalisées. Le laboratoire n'étant pas équipé d'un réfractomètre nous ne pouvons pas le mesurer et avons donc pu que nous référencer à des recherches faites sur le mélange utilisé pour augmenter l'indice de réfraction de l'eau.
Nous avons également gardé la courbe mesurée avec la fibre dans de l'eau, et ressoudé les deux fibres monomodes ensemble afin d'observer les pertes et pouvoir les soustraire aux pertes que l'on a avec la fibre multimode soudée au milieu.
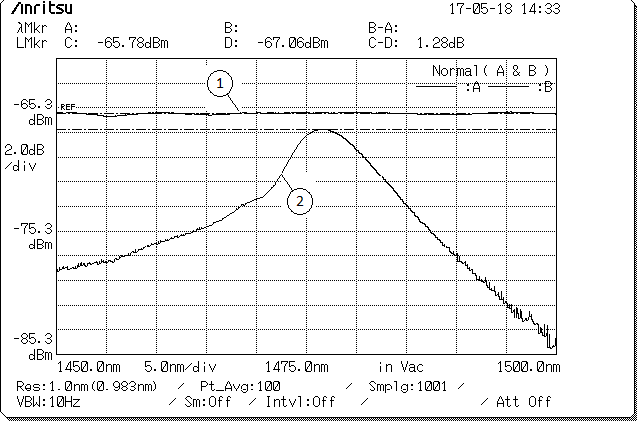
Figure 5 : Spectre de l'intensité (dB) en fonction de la longueur d'onde (nm) SMF-SMF (1) n=1,33 (2)
Nous avons grâce au spectre obtenu (figure 4) mesuré la différence de hauteur en intensité pour le pic à l'indice de l'eau et pour la courbe avec seulement les deux fibres monomodes reliées ensemble. Nous avons donc un écart de 1,28 dB qui correspond environ aux pertes que l'on a lorsqu'on réalise les simulations numériques.
Analyse
Nous avons effectué une mesure du spectre pour chaque solution d'indice différent, et à chaque fois mesuré la position du pic en longueur d'onde.
Nous obtenons donc le tableau de données suivant :
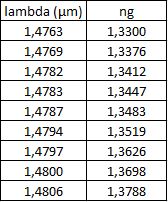
Figure 1 : Tableau de la position du pic et des valeurs d'indice de chaque solution.
Finalement avec ce tableau nous avons tracé l'indice en fonction de la position du pic en longueur d'onde :
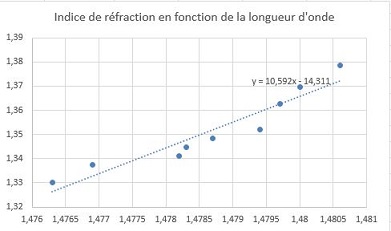
Figure 2 : Courbe de l'indice de réfraction en fonction de la position du pic (µm)
La première remarque et que nous pouvons approximer la courbe à une droite, contrairement à la courbe que nous avions tracée dans la partie simulation où elle avait l'allure d'un logarithme. Ceci est dû au fait qu'ici notre indice varie de 1,33 à presque 1,38 ce qui correspond à la première partie quasi-linéaire de la courbe que nous avions obtenue. Nous remarquons qu'il y a une incertitude : les points sont très souvent hors de la droite de régression linéaire. Ceci peut être dû à un manque de précision dans les mesures ou encore à cause de l'incertitude sur la valeur exact de l'indice de réfraction de nos solutions salées préparées. Cette courbe nous donne une équation qui doit nous permettre de retrouver l'indice de réfraction en remplaçant le x par la longueur d'onde du pic mesuré en µm.
Dans notre tableau (figure 1) nous avions par exemple pour une longueur d'onde de 1,48 µm, un indice de réfraction de 1,3698. Si nous effectuons le calcul avec notre équation de droite pour cette longueur d'onde nous avons : 10,592 x 1,48 -14,311 = 1,36516. Nous obtenons donc des valeurs assez proches Nous pouvons ensuite calculer la sensibilité en prenant l'inverse de la penste ; 1/10,592 = 0,094 µm soit environ 94 nm par unitité d'indice de réfraction.
Comparaison numérique de nos résultats →

