Interférences et ré-imagerie
Les interférences
Les modes se propagent avec des constantes de propagation βm différentes et ainsi la vitesse de phase est différente également, ces modes vont donc interférer constructivement lorsqu’ils sont en phase et déstructivement dans le cas contraire.
Nous utilisons la formule de l'article [2] suivante:
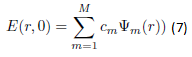
E(r,0) est la somme de tous les champs de la fibre multimode en z = 0, Ψm(r) est le champ dans la fibre multimode du mode LP0,m et Cm est un coefficient d’excitation de chaque mode propre. Nous supposons que le champ de l'unique mode de la fibre monomode soit égal à la somme de tous ces modes de la fibre multimode.
Nous traçons le champ E (r,0) et Ψ0 (r) (Ici E(r,0) est la somme sur le champ des modes LP0,m de la fibre multimode, et Ψ0 est le champ dans la fibre monomode d’entrée) pour vérifier l’égalité de la formule (7). Nous constatons que les deux courbes ci-dessous se rapprochent l’une de l’autre. Tous ces résultats ont été obtenus en gardant la même distance (z=0).
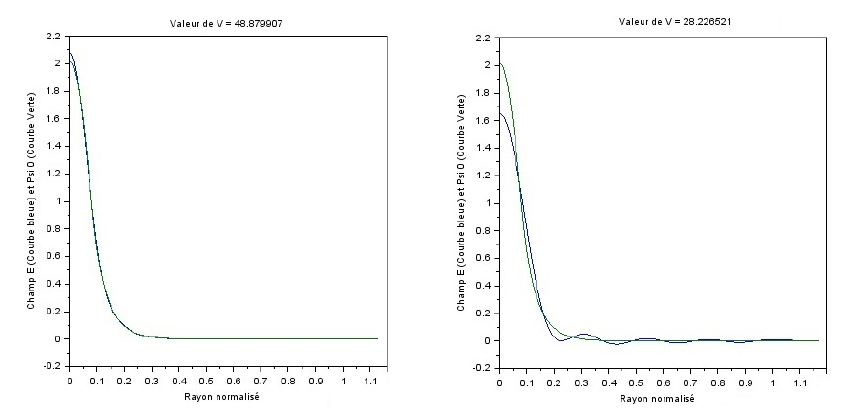
Courbes des modes LP0,msuperposés en fonction du rayon normalisé de la fibre (V différent, z=0)
Sur le graphique de droite sur l'image ci-dessus, nous remarquons que les deux courbes sont moins bien superposées: plus V est grand, plus les courbes seront proches. Nous pouvons interpréter ceci par le fait que nous avons considéré qu'il n'y avait pas de perte, alors qu'il doit sûrement y en avoir et c'est ce qui pourrait expliquer que les deux courbes ne se supperposent pas parfaitement. Cette simulation que nous avons effectuée, nous permet de comprendre la théorie, et de visualiser le comportement des modes ; nous permettant de fabriquer un capteur d'indice de réfraction performant et fiable.
Nous avons, pour le champ à une distance z dans la fibre multimode, l’équation suivante :
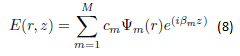
La ré-imagerie
Le concept de « ré-imagerie », ou plus précisément ce qu’on appelle la distance de « ré-imagerie » dans une fibre multimode, est la distance où tous les modes ayant une constante de propagation différente, interfèrent constructivement entre eux et que l’on retrouve la même intensité que celle présente à l’entrée de la fibre multimode, où rentre la lumière. On parle alors de recouplage des modes dans la fibre monomode. Ainsi après avoir soudé une fibre monomode à une fibre multimode, il faut déterminer la longueur de la fibre multimode nécessaire pour avoir ré-imagerie du mode excitateur de la fibre multimode.
Nous avons donc la formule suivante tirée de l'article [2], qui permet de calculer les pertes lors du recouplage des modes de la fibres multimode dans l'unique mode de la fibre monomode de sortie :
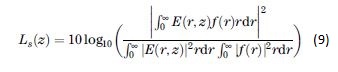
Avec f(r), le mode fondamental de la fibre monomode.

