Structure des fibres et Modes linéairement polarisés
La structure des fibres optiques
Pour bien comprendre les fibres optiques, il faut tout d’abord commencer par comprendre leur structure et composition. Une fibre optique peut être réalisée à l’aide de différents matériaux et ceci impliquera des phénomènes physiques différents observés par la suite.
Classiquement une fibre est constituée de 3 parties : Le cœur, la gaine optique et la couche protectrice.
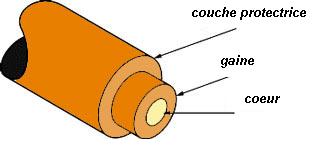
Schéma succinct d’une coupe transversale d’une fibre optique
Description détaillée des différentes parties d’une fibre :
- Le cœur constitue l’une des parties où se trouve la lumière, et c’est cette partie qui a le diamètre le plus petit. La lumière n’est que partiellement confinée dans celui-ci. La fibre est souvent faite de verre ou plastique mais très souvent constituée avec de la silice.
- La gaine optique constitue une fine couche qui entoure le cœur de la fibre optique, elle joue un rôle tout aussi important que le coeur de la fibre pour la propagation des ondes lumineuses. Elle est généralement en silice comme le cœur mais avec un indice de réfraction légèrement inférieur à celui-ci.
- La couche protectrice est une couche en plastique qui offre une protection supplémentaire à la fibre contre les perturbations extérieures qui pourraient être engendrées.
Les modes linéairement polarisés
Pour décrire la propagation de la lumière dans une fibre, nous avons utilisé la théorie sur les modes de propagation dits linéairement polarisés LPl,m.
Pour étudier les différents modes qui sont « excités » dans la fibre optique nous avons besoin de faire appel aux équations de Maxwell, et à partir de ces équations en déduire les équations de propagation associées. Et enfin de chercher les solutions qui sont décrites grâce aux fonctions de Bessel.
Nous allons tout de suite présenter les résultats des solutions des équations de propagation, le développement des calculs des équations de Maxwell et des équations de propagation est visible dans le chapitre 4 du Rapport .
Nous avons ainsi le champ transverse qui s'exprime comme suit, en coordonnées cylindriques (r , Φ, z) :
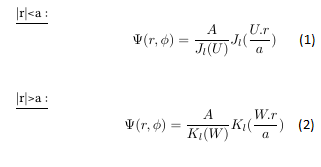
avec r/a le rayon normalisé de la fibre et l'axe z correspondant à l'axe longitudinal de la fibre.
Nous avons les équations caracatéristiques avec les fonctions de Bessel J et K suivantes :
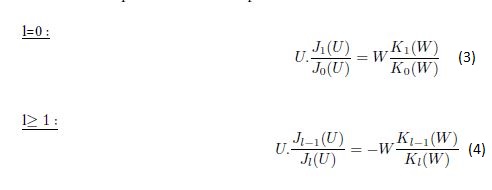
Avec :
J et K les fonctions de Bessel
V la fréquence normalisée
U et W des paramètres définis comme-ci : U = a √(k02 nc2 - β2) et W = a √(β2 - k02 nc2)
β la constante de propagation
k0 le vecteur d'onde (=2π/λ0)
Et b la constante de propagation normalisée définie comme-ci :
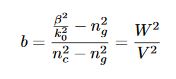
Nous pouvons donc écrire U et W comme : U = v √(1-b) et W = v √(b)
Modes LP0,m
Pour notre projet, nous nous intéresserons surtout aux modes LP0,m car lorsque le mode LP01 de la fibre monomode va se propager et arriver à la première jonction avec la fibre multimode, seuls les modes avec l=0 (LP01, LP02, LP03, …) pourront être excités et se propager dans la fibre multimode. Ceci est dû au fait que nous supposons que la fibre est de symétrie circulaire et que l'alignement axial du coeur des deux fibres est idéal. Ainsi le mode de la fibre monomode sera de symétrie cylindrique et ne pourra se recoupler qu'avec les mode LP0,m, le calcul des intégrales avec les autres modes étant nul.
Nous avons donc Ψ(r ; Φ) = R(r) car l = 0
et donc le champ transverse d’un mode se réduit à sa partie radiale. Si on étudie le champ à un instant
t donné en fonction de la distance z parcourue, nous avons la phase qui ne dépend plus que de βz et on a donc pour la propagation d'un mode :
![]()
Nous avons réalisé des simulations numériques avec le logiciel Scilab, nous avons utilisé pour réaliser cette simulation l’article [2]. Ce programme a pour but de simuler la propagation des modes dans les fibres optiques, et plus particulièrement ici dans la structure appelée SMS c'est à dire SMF-MMF-SMF.
Détermination des valeurs de b
Nous prenons l'équation (3) et la modifions, ainsi nous définissons une nouvelle équation g qui sera :
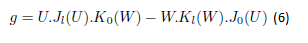
Cette équation nous permet de trouver les valeurs de la constante de propagation normalisée b, nous cherchons lorsque l'équation g est égale à zéro. Nous traçons donc avec le logiciel Scilab, le logarithme de la fonction g et cherchant lorsque celle-ci s'annule pour certaines valeurs de b. Sur la figure ci-dessous, les valeurs de b pour lesquelles l'équation est nulle sont représentées par les pics.
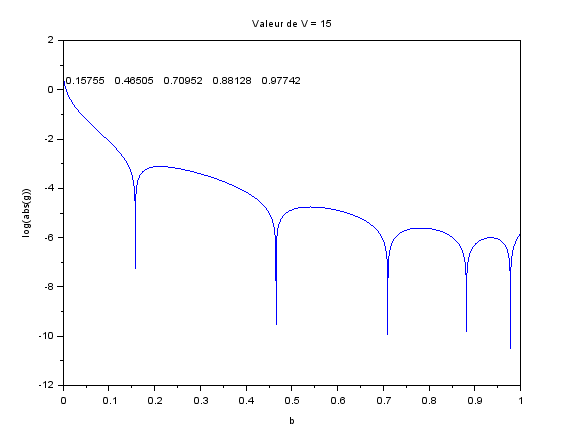
Figure 1 : Graphique du logarithme de g en fonction des valeurs de la constante de propagation normalisée b
Nous traçons ensuite le champ Ψ en utilisant les formules pour le champ, en fonction du rayon normalisé. Le champ est normalisé à 1 à l'interface coeur-gaine et nous supposons que la fibre est parfaitement cylindrique (donc pas de dépendance en Φ), avec chaque courbe qui représente un mode :
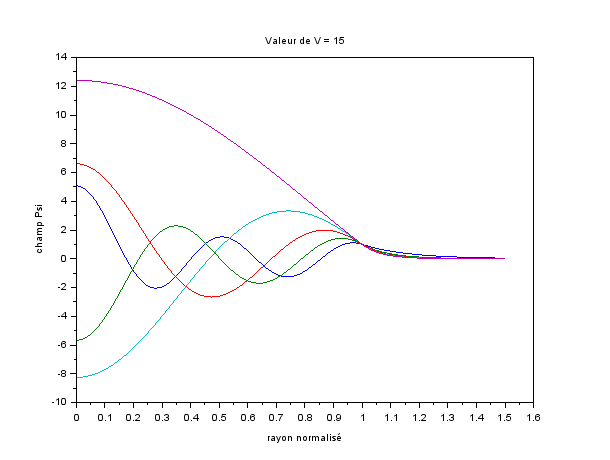
Figure 2 : Champ ψ en fonction du rayon normalisé

