Simulations numériques post-expériences
Cette simulation a été réalisée une fois que toutes les expériences avaient été effectuées.
Determination d'une longueur z optimale
Nous avons d'abord modifié un paramètre dans notre programme ; le rayon du coeur de la fibre multimode dont nous avons mesuré à l'aide d'un palmer le diamètre qui est de 121 µm. Nous entrons donc dans notre programme un rayon de 60,5 µm et nous fixons la longueur d'onde à 1550 nm, nous fixons également l'indice à celui de l'eau (1,33) et nous faisons varier la longueur z.
Ceci nous permet de tacer une courbe de l'intensité en fonction de la longeur z de la fibre multimode.
Nous obtenons donc le graphique suivant :
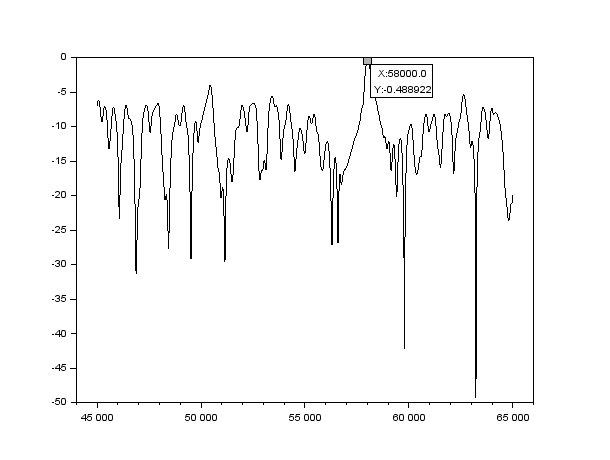
Figure 1 : Graphique de l'intensité (dB) en fonction de la longueur z (en µm)
Nous voyons que l'on a un pic qui se distingue nettement des autres fluctuations, celui-ci se situe à une longueur z qui vaut 58000 µm, soit environ 58 mm.
Variation de l'indice de la gaine
Nous traçons maintenant non plus le spectre en fonction de la longueur z, mais en fonction de la longueur d'onde.
Pour cela, nous fixons le longueur z que nous avons déterminé graphiquement auparavant (58000 µm), et l'on fait varier la longueur d'onde de 1450 nm à 1500 nm, étant la gamme où se situent les pics.
Enfin comme précédemment, nous fixons l'indice à plusieurs valeurs, entre 1,33 et 1,37 en traçant à chaque fois la spectre de l'intensité en fonction de la longueur d'onde. Nous pourrions aller au-delà pour l'indice, dans notre modèle numérique nous pouvons nous rapprocher jusqu'à 1,44 mais comme nous l'avons précisé auparavant (Préparation des solutions salées), nous sommes limités par la technique employée pour réaliser des solutions de différents indices de réfraction.
Nous obtenons ainsi le spectre suivant :
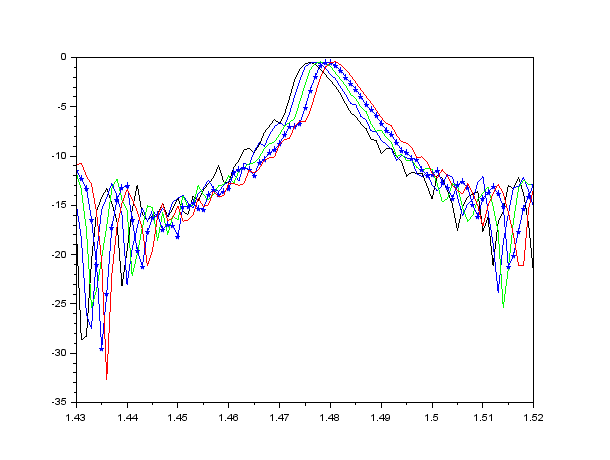
Figure 2 : Spectre de l'intensité (dB) en fonction de la longueur d'onde (en µm)
nnoir=1,33 ; nbleu=1,3416 ; nvert=1,3519 ; nbleu2=1.36264 ; nrouge=1,3698.
Sur le spectre, nous avons tracé les courbes pour différents indices, de gauche à droite nous avons comme indice : 1,33 1,3416 1,3519 1.36264 1,3698.
Nous remarquons donc bien que lorsque nous augmentons l'indice de réfraction la courbe se décale vers la droite.
Nous traçons ensuite également des spectres pour voir les décalages suivant différents indices de réfraction en comparant à chaque fois avec la courbe de l'indice de réfraction de l'eau (1,33) comme référence.
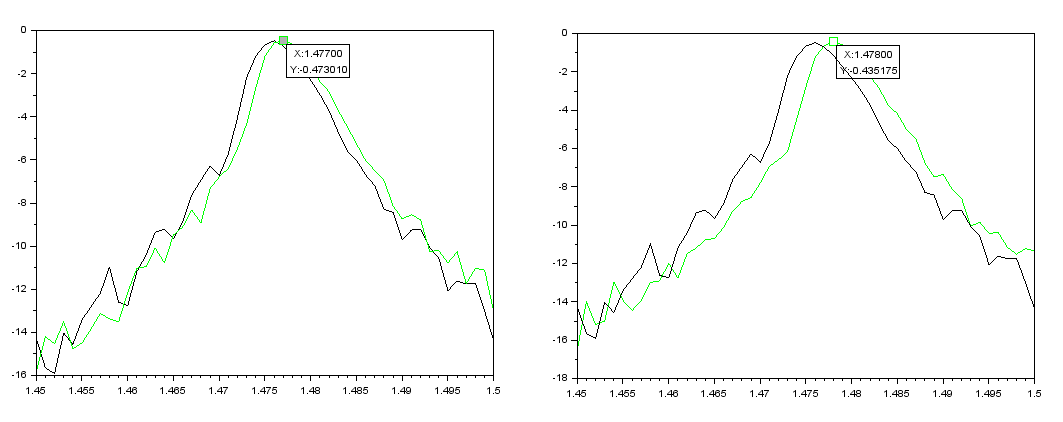
nnoir=1,33 nvert=1.3412 nnoir=1,33 nvert=1,3519
Figure 3 : Spectres de l'intensité (dB) en fonction de la longueur d'onde (en μm)
Avec sur le spectre à gauche : l' indice de réfraction 1,33 pour la courbe noire et 1,3412 pour la verte.
Sur le spectre à droite : l' indice de réfraction 1,33 pour la courbe noire et 1,3519 pour la verte.
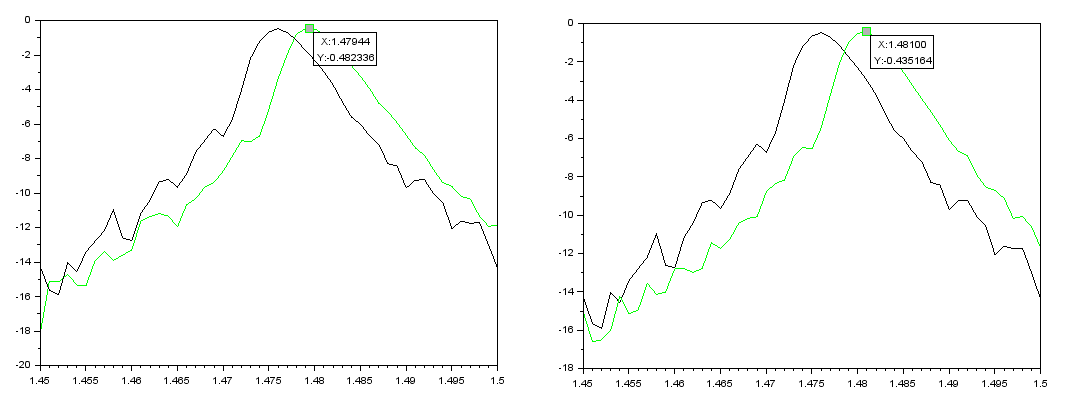
nnoir=1,33 nvert=1.3626 nnoir=1,33 nvert=1,3698
Figure 4 : Spectres de l'intensité (dB) en fonction de la longueur d'onde (en μm)
Avec sur le spectre à gauche : l' indice de réfraction 1,33 pour la courbe noire et 1,3626 pour la verte.
Sur le spectre à droite : l' indice de réfraction 1,33 pour la courbe noire et 1,3698 pour la verte.
Pour l'indice de réfraction de l'eau 1,33 le pic se situe à une longueur d'onde de 1476 nm, nous pouvons constater que plus l'indice de réfraction augmente plus les pics se décalent vers les grandes longueurs d'onde.
Finalement avec ces valeurs nous avons tracé l'indice en fonction de la position du pic en longueur d'onde :
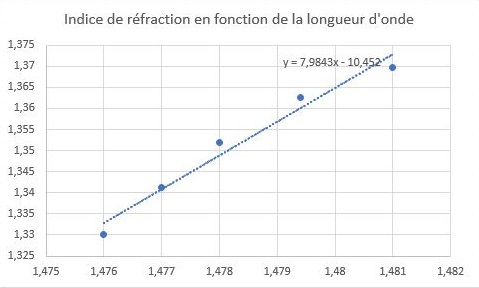
Figure 5 : Courbe de l'indice de réfraction en fonction de la position du pic (µm)
Nous pouvons donc également calculer la sensibilité du capteur pour la simulation ; 1/7,9843 = 0,128 µm soit environ 128 nm par unité d'indice de réfraction. La valeur que l'on trouve est supérieure à la valeur trouvée avec la courbe expérimentale (94 nm par unité d'indice de réfraction), la sensibilité du capteur est donc plus importante dans le modèle numérique que pour notre capteur, c'est un résultat auquel nous pouvions nous attendre

