Simulations numériques pour le capteur
Le but de notre projet est de fabriquer un capteur d'indice de réfraction pour un liquide, en soudant une fibre multimode, d'une certaine longueur, entre deux fibres monomodes. La fibre multimode sera immergée dans le liquide dont on souhaite connaître l'indice de réfraction. Cette simulation numérique a pour but de déterminer, et d'observer, les spectres obtenus pour différents indices de réfraction, c'est à dire différents indices de liquides dans lesquels la fibre baignera expérimentalement.
Ceci nous permettra de trouver une relation entre l'indice du liquide et le déplacement de la position du pic sur le spectre (en longueur d'onde).
Determination d'une longueur z optimale
Nous commençons par tracer un graphique pour déterminer la longueur de fibre multimode qui nous sera nécessaire.
Pour cela, nous fixons la longueur d'onde à 1550 nm, nous fixons également l'indice à celui de l'eau (1,33) et nous faisons varier la longueur z. Le rayon pour la fibre multimode utilisé ici est 62,5 µm
Nous obtenons donc le graphique suivant :
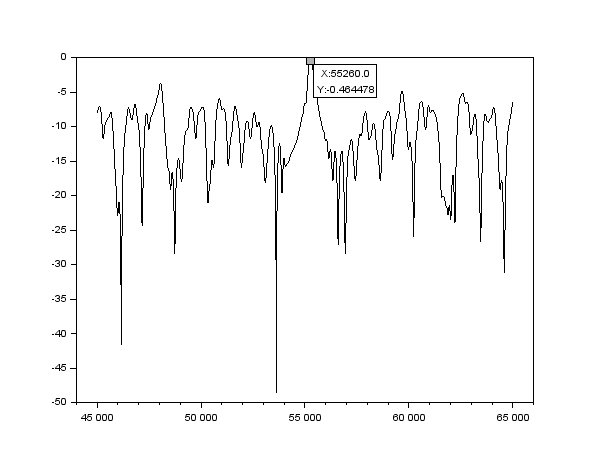
Figure 1 : Graphique de l'intensité (dB) en fonction de la longueur z (en µm)
Nous voyons que l'on a un pic qui se distingue nettement des autres fluctuations, qui correspond à la première distance de ré-imagerie. Celui-ci se situe à une longueur z qui vaut 55260 µm, soit environ 55.3 mm.
Variation de l'indice de la gaine
Nous traçons maintenant non plus le graphique en fonction de la longueur z, mais en fonction de la longueur d'onde.
Pour cela, nous fixons le longueur z, que nous avons déterminé graphiquement juste avant (55260 µm), et l'on fait varier la longueur d'onde de 1450 nm à 1650 nm.
Enfin comme précédemment, nous fixons l'indice de la fibre multimode à plusieurs valeurs, entre 1,33 et 1,43 en traçant à chaque fois la spectre de l'intensité en fonction de la longueur d'onde.
Nous obtenons ainsi le spectre suivant :
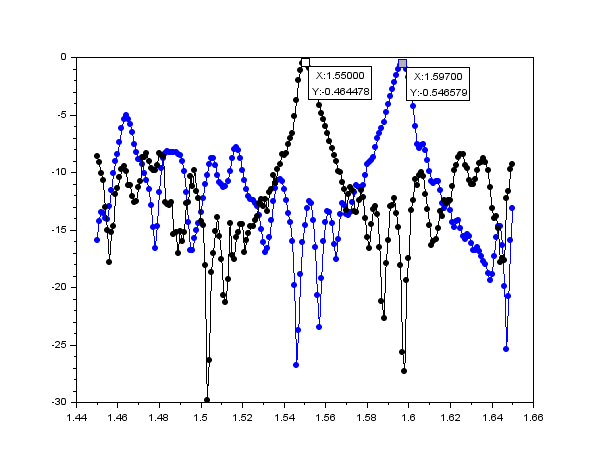
Figure 2 : Spectre de l'intensité (dB) en fonction de la longueur d'onde (en µm)
nnoir=1.33 et nbleu=1.43
Sur le spectre, nous avons en noir la courbe pour l'indice de réfraction à 1,33 et en bleu la courbe pour 1,43. Ceci représente à peu près les limites de mesures pour notre capteur, on remarque bien que lorsque nous avons augmenté l'indice de réfraction la courbe s'est décalée vers la droite, ici elle s'est décalée de 47 nm.
Nous traçons ensuite également des spectres pour voir les décalages suivant différents indices de réfraction.
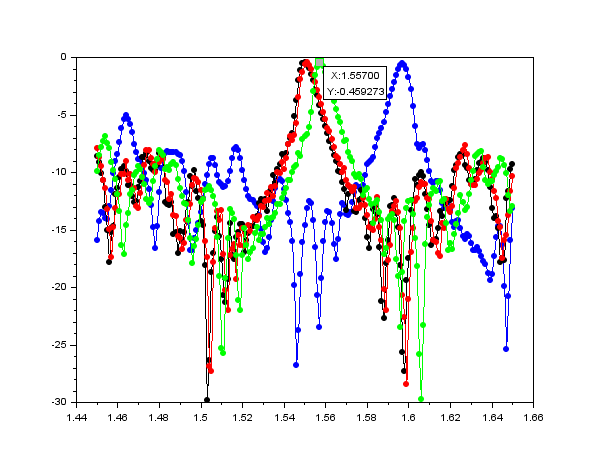
Figure 3 : Spectre de l'intensité (dB) en fonction de la longueur d'onde (µm), nnoir = 1.33, nrouge = 1.34, nvert = 1.38 et nbleu = 1.43
Pour l'indice 1,33 le pic se situe à une longueur d'onde de 1550 nm, ici nous avons pour la courbe verte un indice de 1,38 et une position du pic à 1557 nm.
Cela nous donne donc un écart de 7 nm pour une variation de 0.05 de l'indice.
En revanche lorsqu'on regarde la variation en longueur d'onde pour l'indice de 1,33 à 1,34 (courbe noir à rouge) la longueur d'onde et respectivement de 1550 nm et 1551 nm.
L'écart ici est donc très faible, et sachant que la résolution de notre appareil de mesure est d'environ 1 nm, nous pouvons penser qu'il sera difficile de determiner l'indice avec une telle précision.
Avec cette simulation, nous avons pu relever l'indice de réfraction correspondant à chaque position du pic. Nous avons donc pu tracer avec le tableur excel une courbe de l'indice de réfraction en fonction de la longueur d'onde du pic.
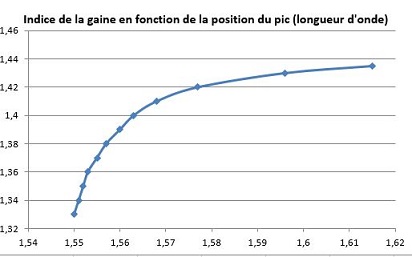
Figure 4 : Courbe de l'indice de réfraction en fonction de la position du pic (µm)
Nous remarquons donc que l'allure de la courbe n'est pas une droite mais ressemble fortement à une fonction comme le logarithme. Nous remarquons également que plus la longueur d'onde est élevée moins l'indice de réfraction varie.

