Résultats théoriques

Le système composé de deux métronomes peut être schématisé ainsi: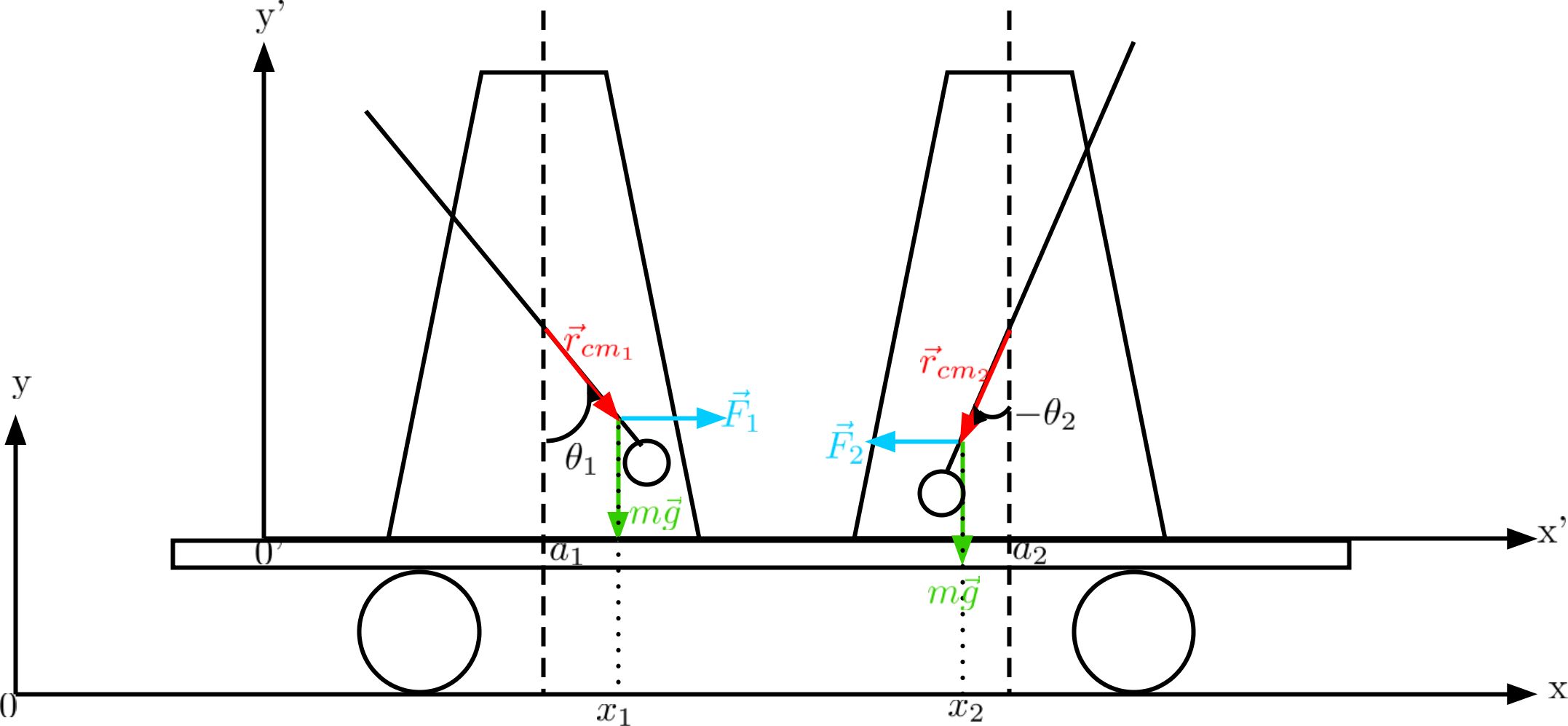



Les équations du mouvement dans le référentiel de la planche sont:
\[ \frac{d^2\theta_1}{dt^2}+\frac{mr_{cm} g}{I} sin\theta_1+\epsilon\left[\left(\frac{\theta_1}{\theta_0}\right)^2 -1\right]\frac{d\theta_1}{dt}-\left(\frac{r_{cm} m cos\theta_1}{I}\right)\left(\frac{mr_{cm}}{M+2m}\right)\frac{d^2(sin\theta_1+sin\theta_2)}{dt^2} =0 \]
\[ \frac{d^2\theta_2}{dt^2}+\frac{mr_{cm} g}{I} sin\theta_2+\epsilon\left[\left(\frac{\theta_2}{\theta_0}\right)^2 -1\right]\frac{d\theta_1}{dt}-\left(\frac{r_{cm} m cos\theta_2}{I}\right)\left(\frac{mr_{cm}}{M+2m}\right)\frac{d^2(sin\theta_1+sin\theta_2)}{dt^2} =0 \]
Afin d'adimensionner ces équations, nous définissons les paramètres suivants:

  • le temps adimensionné $$\tau = \omega t$$
  • la fréquence moyenne $$ \omega^2= \frac{mr_{cm}g}{I}=\left(\frac{\omega_1+\omega_2}{2} \right)^2 $$
  • la différence de fréquence $$\Delta=\frac{\omega_1-\omega_2}{\omega}$$
  • le terme de couplage des masses $$\beta=\left(\frac{mr_{cm}}{M+2m}\right)\left(\frac{mr_{cm}}{I}\right)$$
  • le coefficient de Van der Pol $$\mu=\frac{\epsilon}{\omega}$$


    • Après adimensionnement, ces équations deviennent:

    \[ \frac{d^2\theta_1}{d\tau^2}+(1+\Delta)sin\theta_1+\mu\left(\left(\frac{\theta_1}{\theta_0}\right)^2-1\right)\frac{d\theta_1}{d\tau}-\beta cos\theta_1\frac{d^2}{d\tau}(sin\theta_1+sin\theta_2)=0 \]
    \[ \frac{d^2\theta_2}{d\tau^2}+(1-\Delta)sin\theta_2+\mu\left(\left(\frac{\theta_2}{\theta_0}\right)^2-1\right)\frac{d\theta_2}{d\tau}-\beta cos\theta_2\frac{d^2}{d\tau}(sin\theta_1+sin\theta_2)=0 \]

    Ces équations ont été le point de départ d'une étude analytique menée en amont. Grâce à la méthode de développement multi-échelle, nous avons montré dans cette étude que le déphasage entre les deux métronomes n'est pas nul mais constant. Il est lié au terme de couplage β, au coefficient de Van der Pol μ et à Δ le désaccord en fréquence des deux métronomes. Ainsi, lorsque ces derniers sont sychronisés et donc dans un état stationnaire, le déphasage est donné par:

    \[ \psi ≈ \arcsin \left(\frac{\mu \Delta}{\beta (3\gamma +\beta)}\right) \]