Incertitudes liées aux points choisis:

Nous allons maintenant supposer la position du canon connue et essayer de déterminer les incertitudes que nous donne le choix des points; c'est-à-dire pouvoir répondre à la question: est-ce que mettre les points dans une certaine configuration nous donnera de plus faible incertitudes que dans une autre?
On pourra donc étudier différents cas parmi les plus généraux qui nous permettrons de mieux comprendre comment varie les incertitudes en fonction des points choisis.

On place les trois points à étudier sur la carte. Nous prendrons ici les deux cas qui nous semblent les plus intéressants à traiter, a savoir : une configuration en ligne des trois points par rapport au canon, ainsi qu'une configuration en arc de cercle des trois points autour du canon, sur le même plan d'onde (n'importe quel cercle ayant le canon pour centre).

              
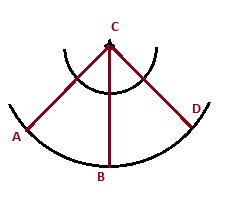
                                                                                    Fig7:Configuration 1                                                 
                         
                               

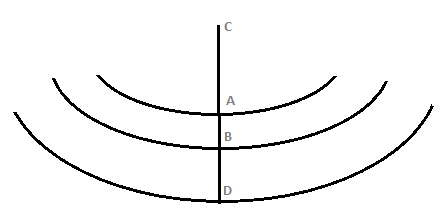
                                                                                      Fig8:Configuration 2     

Avant de faire le calcul, étudions ces configurations, nous pourrons ainsi comparer nos résultats avec ce que nos prévisions.
On peut se dire par exemple que la configuration 1 donnerait des grandes incertitudes car les différences de temps seraient très faibles entre les trois observateurs étant donné qu’ils se trouvent sur le même plan d’onde.
De même on peut penser que la configuration 2 serait plutôt bonne pour les incertitudes car on aurait alors des différences de temps plus grandes entre nos observateurs.

Cependant, après les calculs on constate que la configuration 1 nous donne un résultat tout à fait acceptable.

Pour la configuration 2 on trouve des incertitudes énormes, bien plus grande que ne l'est la dimension de notre carte. Nous allons donc essayer de comprendre cela en appliquant la "méthode semi-numérique". Les solutions de la position du canon seront en fait données par une demi-droite partant du point A et dirigée vers le canon. La "méthode géométrique" nous donnera la même chose, car cela reviendrai à prendre pour solution l'ensemble des centres des cercles passant par le point A et tangent au deux cercle passant par celui-ci (de rayon CB-CA centré en B et de rayon CD-CA centré en D), donc la demi-droite évoqué précédemment.
On pourrait expliquer de si grandes incertitudes pour la configuration 2 en pensant au fait que dans notre repère on aurait plus aucune coordonnées suivant y ce qui entraîne peut être cela. De plus les hyperboles tendent vers une droite lorsque les points tendent vers l’alignement (voir schéma ci-dessous)

 

 

 

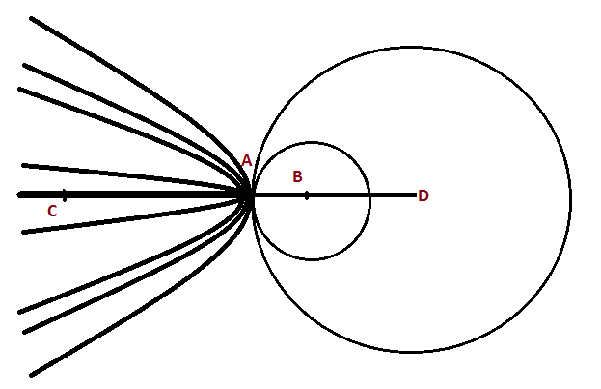
                                    Fig9:Schéma des hyperboles tendant vers une droite et représentation des cercles.