Méthode numérique :

Nous allons nous intéresser maintenant à une méthode plus moderne, nécessitant l'intervention d’ordinateur pour résoudre les équations mathématiques caractérisant le problème.

Mise en équation :

On a vu précédemment que :  

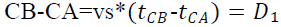
et sachant que D₁ est constant (comme expliquée dans (I)) pour des points donnés, il nous reste donc à traduire la partie CB-CA en équation a l'aide d’un repère judiciairement choisi, permettant de simplifier l’équation au maximum. Pour cela nous considérerons le point A comme origine du repère, et le point B sera choisi de telle sorte que la distance AB va être  l'unité de ce repère, le point D dont les coordonnées (α, β) sont connues, et exprimées en fonction de l'unité de notre repère, et enfin le canon de coordonnées (x,y)  qu'on trouvera grâce au programme.
Nos points choisi dans la méthode géométrique nous donnerons les résultats suivant (en unité du repère toujours): α=0.56, β=1.18, D₁=0.179  et D₂=0.930
Le schéma suivant décrit nos trois points et notre canon:

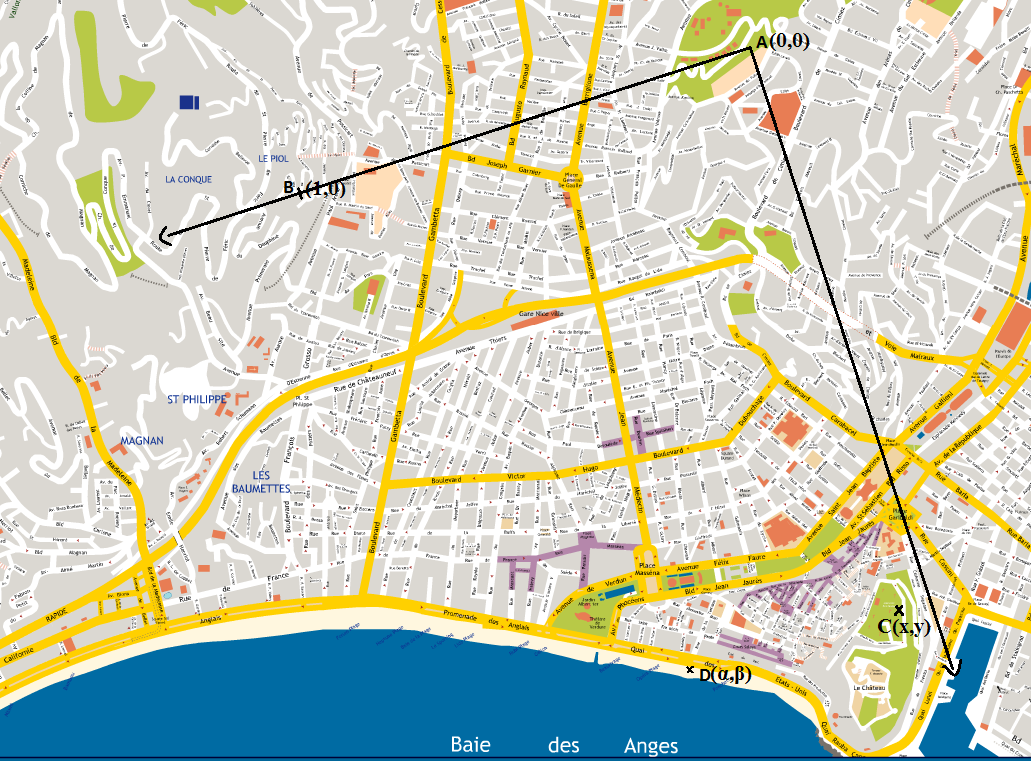
                                              Fig3:positionnement des trois observateurs et tracé du repére

                                                                  (cliquer sur l'image pour agrandir)

Sachant que :

On trouve :

D’où :                   

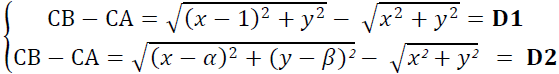
On obtient alors deux équations à deux inconnus : un système soluble. C’est pour cela qu’il faut trois observateurs, afin d’obtenir deux équation a deux inconnues et non une seule équation a deux inconnus (insoluble) si il n’y avait eu que deux observateurs.

Nous avons donc un système de la forme :

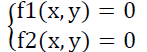
 Qu’on mettra dans un programme informatique pour le résoudre.

En entrant toutes les équations dans le programme, celui-ci nous donne (x,y) les coordonnées de la position du canon en unité du repère choisi. Cependant en itérant sur plusieurs point de départ, on constate qu’il n’y a pas qu’une seule solution a notre système mais quatre. Pour notre exemple on trouve les solutions: (0.26, 1.20); (0.66, –0.74); (0.70, 0.96); (0.40, –0.20) que l'on pourra comparer avec d'autres méthodes.

Pourquoi en trouve-t-on quatre ? Et comment pouvons nous distinguer la bonne solution ?
Sont alors les questions que nous nous sommes posées, la réponse de la première sera développée par la suite dans la partie " Méthode semi-numérique" car cela relève d’une compréhension graphique des équations. En ce qui concerne la deuxième question, en plaçant les 4 points sur la carte, et en comparant nos résultats sur les temps mis par le son pour aller en A,B et D, nous pourrons savoir en quel point le son arrive en premier ,en deuxième et en troisième, et en déduire la solution acceptable parmi les quartes, sinon ,on peut toujours utilisé la méthode graphique vue précédemment qui donne une idée sur l’endroit ou se trouve le canon.
Ces techniques nous permettent de localiser le canon, mais avec quelle précision ?

La méthode numérique donne un assez bon résultat car elle nous permet d’avoir directement les coordonnées du canon (sans qu'il y est d'autres erreurs liées aux tracés ou autres).

Nous traçons les résultats que nous avons obtenus après plusieurs mesures sur le schéma suivant:

 

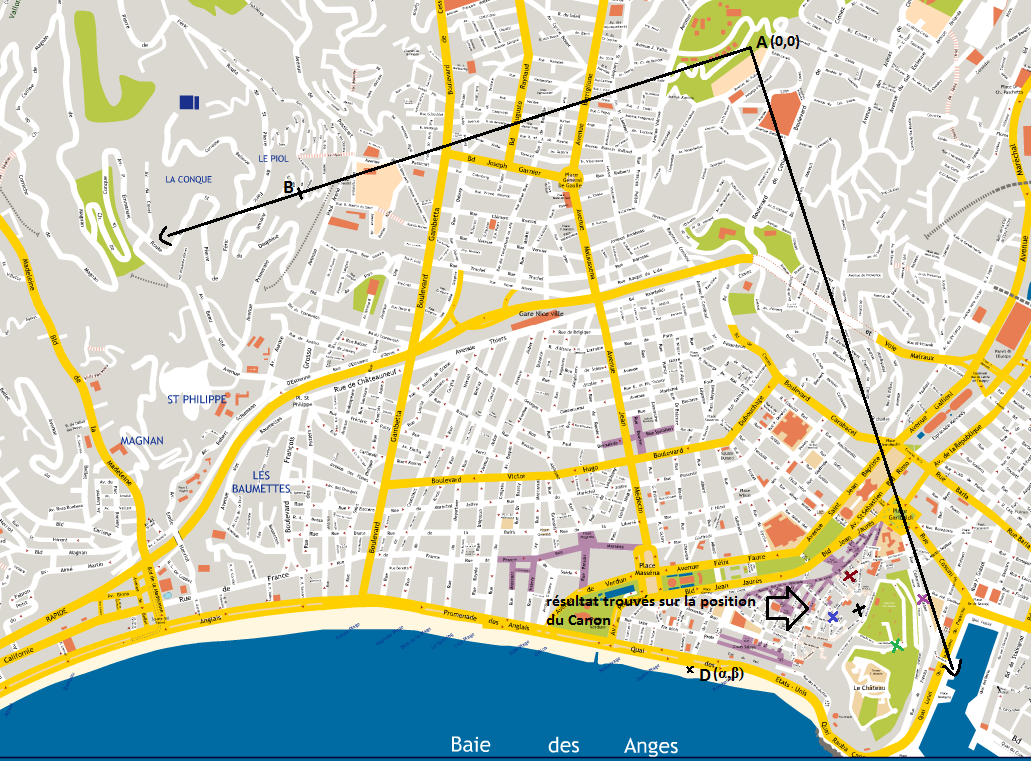
                                            fig4:Placement des positions du canon pour différentes mesures

                                                                    (cliquer sur l'image pour agrandir)

Les  résultats trouvés sont plutôt acceptable et proche les uns des autres, on comparera ceux-ci
avec le losange d'erreur obtenu par la suite.