Etudes des incertitudes expérimentale :

Nous allons étudier ici la précision avec laquelle on obtient  notre résultat sur la position du canon; c’est-à-dire déterminer les incertitudes sur x et y, notées respectivement Δx et Δy.

1) incertitudes rencontrées :

On va commencer par  étudier  les incertitudes dues aux mesures, c’est-a-dire, a notre temps de réaction vis-à-vis du chronomètre, ainsi que l'incertitude sur la vitesse du son.
On cherchera donc à déterminer l'incertitude sur la distance CB-CA et CD-CA :

Sachant que :                                 

 

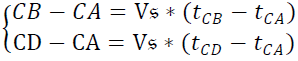
On trouve :
                   

                                                    
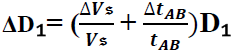
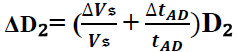
Il faudra déterminer donc les incertitudes sur la vitesse du son ainsi que l’erreur expérimentale sur nos différences de temps.
En ce qui concerne l'incertitude sur le temps, elle dépend de notre temps de réaction lors de l'entente du son, nous avons donc essayer de reproduire les conditions de prise de mesure en salle  pour ainsi pouvoir connaître approximativement nos différences de temps de réaction a l'entente du son. Ainsi l’un de nous trois donnait le signal alors que les deux autres attentifs (l'attention est importante pour minimiser les écarts que nous avons entre nous car ce sont des différences de temps que nous regardons ici) appuyaient sur le bouton pour arrêter le chronomètre dès l’entente de celui-ci. En faisant une soixantaine de mesure, et en calculant la moyenne de celles-ci on trouve une incertitude d’environ un dixième de seconde : Δt≈0.1s
Pour l'incertitude sur la vitesse du son (on parle de la vitesse et non de l'intensité) le seul facteur pouvant joué un rôle important est la température, or on faisant attention à la température pendant les mesures et en constatant qu’on ne s’est pas trouvé au delà de 5 °C de différence par rapport aux mesures précédentes, le terme ∆Vs/Vs est négligeable. On obtient donc:

Apres calcul on trouve : ΔD₁≈ΔD₂≈0.02 u                      

De la même manière que pour D₁ et D₂, on peut montrer que  ΔD₁ et ΔD₂ sont constants pour des points choisis

Nous pouvons aussi parler des incertitudes liées aux différences de hauteur. En effet nous considérons partout que nous travaillons en deux dimensions, ce qui n'est pas vrai car le canon se trouve sur une colline d'une cinquantaine de mètre de haut ce qui nous rajoute environ un mètre sur la distance CD (du canon au point D) ce qui est négligeable.

2) mise en équation des incertitudes :

Sachant que f₁ et f₂ dépendent de x, y ainsi que D₁ (pour f₁) et D₂ (pour f₂), on pourra donc écrire le système suivant faisant intervenir les dérivées partielles de nos fonctions ainsi que les incertitudes associées à x,y et D₁ et D₂.

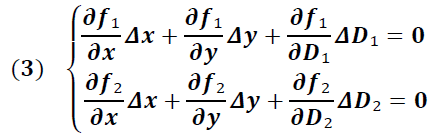
Comme précédemment on fait résoudre le système trouvé (après avoir calculé les dérivées partielles à la main) par un programme informatique. En exécutant celui-ci, il nous  renvoie alors Δx et Δy (ΔD₁ étant connu maintenant), ce qui nous permet de connaitre la précision avec laquelle nous déterminons la position de notre canon. Ainsi dans notre exemple on trouve Δx ≈ 70 mètres et Δy ≈ 135 mètres.