Méthode semi-numérique:

Dans cette partie on analysera le rendu graphique des équations trouvées, ainsi on essayera de répondre a une question importante apparue dans la partie «méthode numérique»: Pourquoi y a-t-il multiplicité des solutions?  Et enfin on étudiera les équations à l'aide d'un programme nous permettant de pouvoir visualiser clairement ce qui se passe.

1) Etude du système :

Nous avons deux équations de la forme f(x,y) = 0. Notre problème de multiplicité des solutions nous a poussé à étudier les solutions graphique des équations de la forme  MB - MA=cste.

On modifie le système, en passant de la forme f(x,y) = 0, à  y = f(x) pour les deux équations.
On trouve :
Pour la première équation :

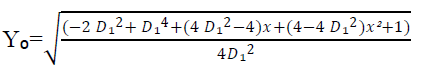
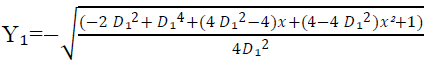
Deuxième  équation :

 

 

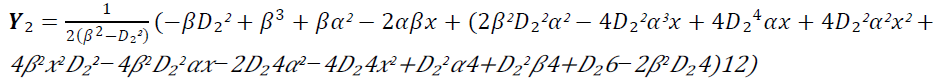
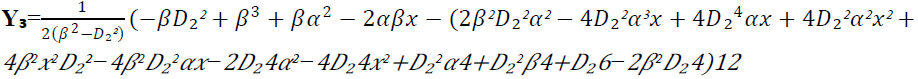
Avec D₁=CB-CA et D₂=CD – CA, et (α, β) les coordonnées du point D.

Or chacune des équations nous donne deux solutions pour y, ce qui revient aux deux branches d'une même hyperbole; cela nous permet donc de comprendre la raison pour laquelle on a quatre solutions.
On peut expliquer la présence de deux branches hyperboles-solutions par équations, par le fait que nous «supprimons» le signe de D₁ et D₂ en mettant au carré le système (1) pour pouvoir le résoudre. Cela «crée» donc la deuxième branche d'hyperboles, que nous pourrons simplifier en regardant le signe de CB-CA et celui de CD-CA c'est-à-dire le signe de D₁ et D₂. En effet si D₁ est positif,
le canon (point C) sera plus proche du point A que du point B car CB sera supérieur à CA; en résonant de même pour D₂ nous pouvons distinguer la bonne solution parmi les quatre que nous trouvons  et ainsi trouver le canon.

 

2) application

On trace y₀, y₁, y₂ et y₃ sur un même graphe pour observer leurs intersections (les unités étant données par celle de notre repère). On trace aussi ces même courbes avec les incertitudes trouvées précédemment ce qui nous donne un losange d'erreur repérant la zone ou pourrait se trouver notre canon compte tenu de nos incertitudes de mesures. Le schéma suivant nous est donné par notre exemple:

 

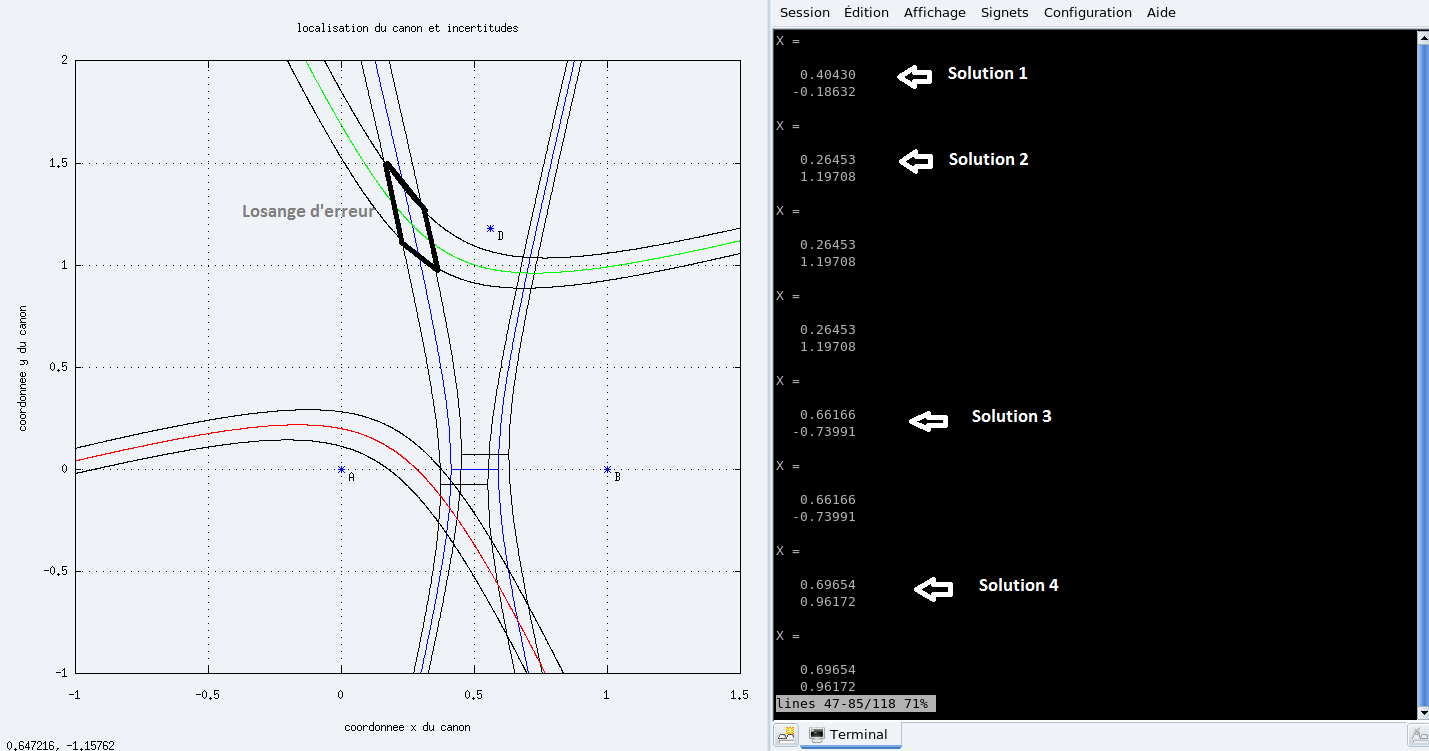
                                                              Fig5:Résultat données par le programme

                                                                   (cliquer sur l'image pour agrandir)

 

On fait le rapprochement avec notre plan de la ville pour mieux se rendre compte de ce que nous montre le programme.

 

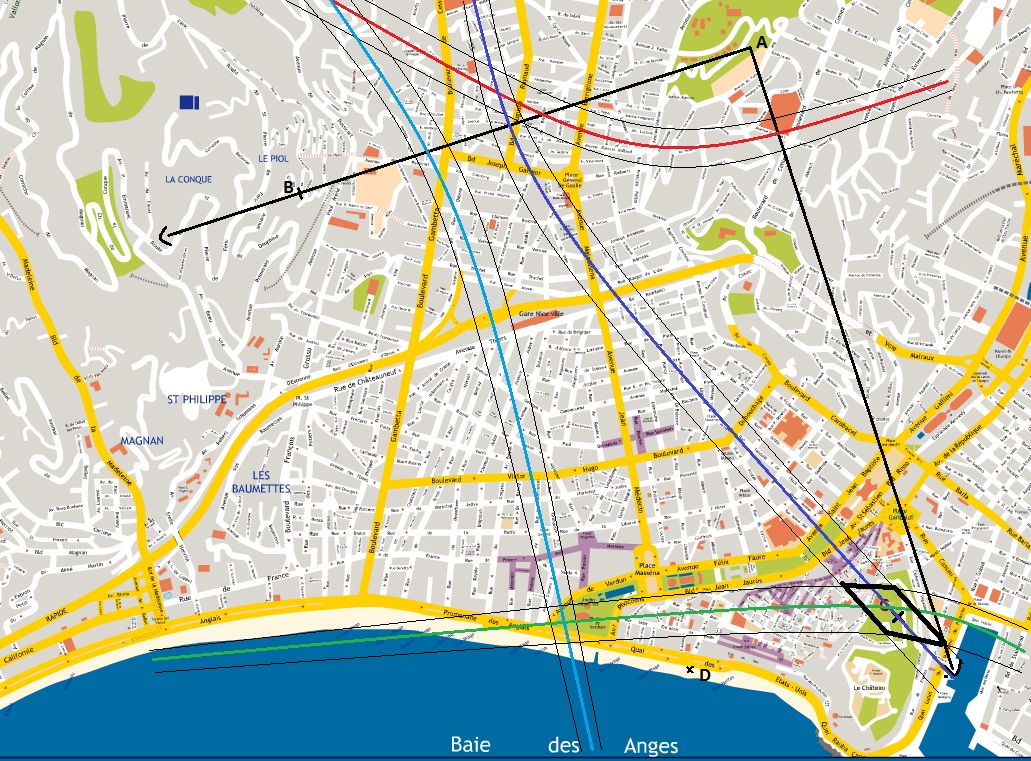
                                                      Fig6:Representation des hyperboles sur un plan de Nice

                                                                     (cliquer sur l'image pour agrandir)

En comparant avec le dernier schéma de la méthode numérique, nous montrant les différentes localisations du canon, on peut voir que celles-ci sont comprise dans ce losange d erreur, ou juste a coté ce qui s’explique par le fait que les losanges sont unique pour chaque mesure et que le losange représentée sur ce schéma correspond a une mesure précise (notre exemple).