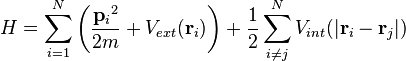
On reconnait ici l'équation de Schrodinger (on nomme d'ailleurs souvent l'équation de Gross-Pitaevskii l'équation de Schrödinger non linéaire) à laquelle on a ajouté un terme non linéaire, où N est le nombre de particules formant le condensat, g est une constante dépendant de la longueur de diffusion de l'atome considéré et ψ² le potentiel d'intéraction entre deux particules. On utilise l'approximation d'Hartree qui permet de considérer la fonction d'onde totale du système comme le produit des fonctions d'ondes d'une particule :

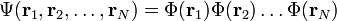
Cette forme pour la fonction d'onde nous assure que toutes les particules sont dans le même état quantique. De plus, la fonction d'onde reste inchangée si on intervertit deux particules. Elle décrit donc naturellement un condensat de Bose-Einstein. On peut donc décrire le condensat comme une onde de matière cohérente.


Une propriété découlant de ce résultat est que deux condensats vont pouvoir interférer entre eux, à la manière des figures d'interférences observés en optique.

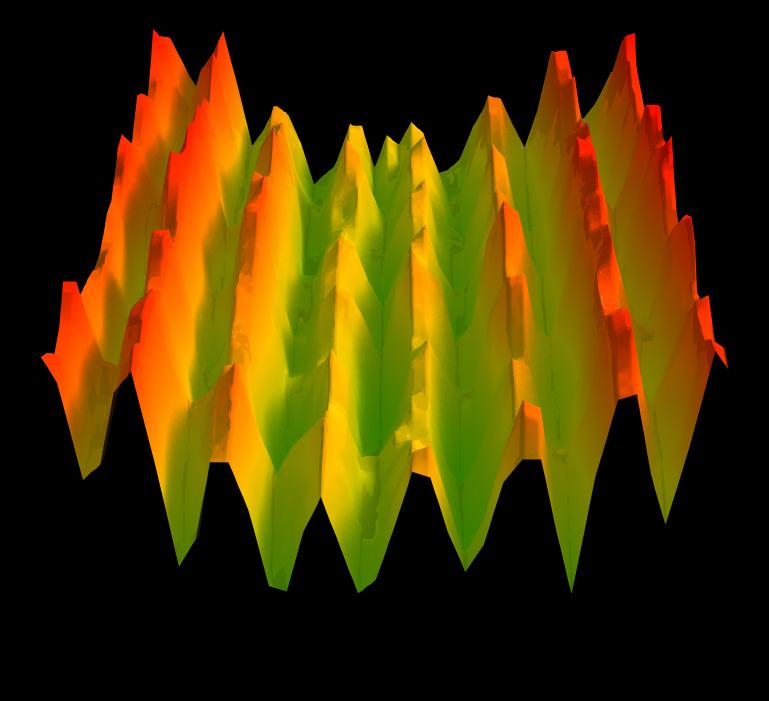
La mise en rotation d'un condensat révèle de manière spectaculaire les contraintes qu'impose la mécanique quantique. Il est impossible de faire tourner un condensat en bloc, à l'image d'un objet classique. La mise en rotation s'accompagne de la création de vortex, c'est-à-dire de lignes le long desquelles la densité est nulle et autour desquelles la circulation de la vitesse est quantifiée.