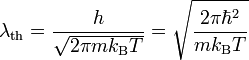
Le terme " v "représentant la vitesse de la particule. Pour observer des effets quantiques dans un gaz de boson, la longueur d'onde associée doit être proche de la distance inter-atome. La température étant lié à la vitesse d'une particule, il va falloir refroidir le gaz à une température de l'ordre de quelques mikroKelvins voir Nanokelvins pour obtenir la bonne longueur d'onde. En d'autres termes, créer un condensat de Bose-Einstein s'avera être un véritable défi technologique et il fallut attendre 1995 pour que l'équipe de Eric Cornell et Carl Wieman y parviennent, recevant le prix nobel en 2001.

Mais refroidir un gaz ne suffit pas à créer un condensat, il faut aussi bien choisir les particules qui vont être utilisées. Comme nous l'avons expliqué, un condensat est un amas de particules qui sont toutes dans le même état quantique. Or Wolgang Pauli en 1925 proposa son principe d'exclusion, interdisant à différents électrons de se trouver dans le méme êtat quantique au même endroit. Paul Dirac, en 1930, élabora ensuite un théorème basé sur ce principe et ainsi naquit la statistique de Fermi-Dirac, nous disant que les particules de spin demi-entier tel que l'électron, les quarks, les neutrinos et plus généralement les atomes dont le nombre de nucléons est impair, subissent le principe d'exclusion de Pauli. Ces particules se nomment les fermions.

L'autre classe de particule sont les bosons, comme par exemple les photons , les gluons et tout les atomes ayant un nombre de nucléons pair. Ces bosons vont obéir à la statistique de Bose-Einstein et pourront, à l'inverse des fermions, être dans le même état quantique au même endroit (citons par exemple les lasers), d'où leur utilisation pour la création de condensats de Bose-Einstein.