Nous allons à présent tenter de faire interagir deux condensats. Nous allons entrer deux fonctions d'ondes. Chaque fonction sera définie par sa masse, m et son potentiel d'interaction interne.

Nous allons placer ces 2 fonctions dans un potentiel harmonique, et voir comment elles interagissent.

Tout d'abords, nous allons définir deux condensats identiques (même masse et même potentiel d'interaction interne) . Nous allons ensuite étudier l'évolution des fonctions d'ondes au cours du temps.

Nous voyons que nos deux condensats se superposent. Lorsque g est suffisament faible, les condensats ne se repoussent pas, et ont les mêmes paramètres. Ils agissent donc comme un seul et même condensat

A présent, nous allons modifier nos paramètres afin d'avoir deux potentiels différents. Nous voulons savoir si le sytème conserve sa symétrie, et si oui, comment. Pour cela, nous allons augmenter la masse de l'un des condensats.

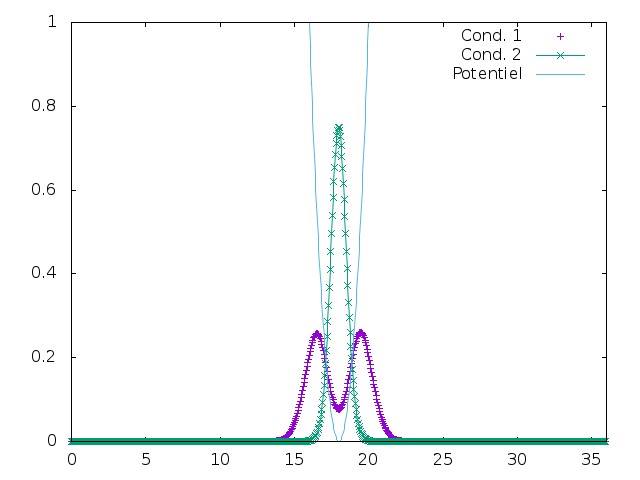
Içi, m1=5*m2... Le condensat 1 est celui au milieu.

Nous observons içi une oscillation du second condensat entre 2 états. Le premier état est un état dit "déphasé". Le condensat le plus léger se trouve répartit de manière symétrique de part et d'autre du système.
Le second état est beaucoup plus instable. C'est l'état dans lequel les condensats se trouvent en "phase". Cet état est très instable à cause de leur répulsion respective. En effet, la répulsion est d'autant plus importante qu'il y a de surface de contact entre eux. Et la superposition des condensats est une position dans laquelle la surface de contact est maximale.

Nous ne pouvons pas savoir si ce système est périodique, nous travaillons avec des équations non-linéaires. De plus, puisque nous travaillons avec une conservation de l'énergie totale du système, il n'y a pas d'atténuation des oscillations. Si nous faisions tourner notre système continuellement, il n'y aurait pas de potition stable dans laquelle les condensats seraient immobiles.

Utilisons notre programme stationnaire pour visualiser ce système :

Nous voyons que le second condensat est centré par le puit de potentiel au même endroit que le premier. Toutefois, il reste repoussé par celui-ci, plus massique. Nous remarquons que plus le rapport de masse augmente, plus les 2 condensats se déphasent

Nous allons à présent vous présenter un cas intéressant, uniquement théorique: les échanges d'énergie entre deux condensats. Pour mettre en évidence les échanges d'énergies , nous allons programmer deux condensats quasi-identiques. Ces condensats sont lâchés dans un environnement libre, sans puit magnétique, et vont donc occuper tout notre espace. On aura alors une solution homogène. Il est important de noter la périodicité aux bords de notre espace. On pourrait comparer cette espace à un "chapeau mexicain", circulaire, dans lequel les condensats s'étaleraient jusqu'à se recouvrir eux-même. Ainsi, par le principe de normalisation de leur fonction d'onde, ces dernières ne seront pas nulles en tout point. D'autre part on perturbe légèrement l'une de nos deux fonctions d'ondes afin d'observer rapidement un phénomène intéressant. En effet, lorsque l'un des condensats va se mettre à osciller, il va être freiné par l'autre, à la manière d'un pendule couplé. Et, de la même manière que cet oscillateur mécanique couplé, il va y avoir un transfert d'énergie d'un condensat vers l'autre. L'oscillation du premier va être freinée, et va engendrer le début d'une oscillation chez le second condensat. Et ce cycle va se répéter a l'infini (conservation d'énergie), à une certaine fréquence.

Nous avons par ailleurs réalisé la même simulation mais avec des masses différentes. On n'observe plus de transfert d'énergie, la différence de masse plaçant les condensats en opposition de phase, dans des "sous-structures".